Обзор существующих методов оценки воздействия подвижного состава на железнодорожный путь

В данном случае перед второй частью равенства поставлен знак минус по причине того, что направление упругого сопротивления давлению с) всегда обратно упругому прогибу, его вызвавшему.

В отечественной практике параметр и — модуль упругости, определяется в большей части экспериментальным путем и данный параметр представляет собой погонный упругий отпор основания, отнесенный к единице прогиба. По мнению Г.М. Шахунянца [41] излишняя жесткость пути увеличивает динамические взаимодействия пути и подвижного состава.Для получения оптимального модуля упругости подрельсового основания его необходимо проектировать, принимая во внимание тот факт, что подрельсовое основание является многослойной конструкцией, необходимо задавать необходимые характеристики каждому слою. В таком случае влияние каждого слоя (подрельсовые прокладки, шпалы, блоки, плиты, путевые маты, подшпальные прокладки и т.п) на общий модуль упругости может быть определено из следующего.

В соответствии с формулами (2.6) и (2.5), через составляющие отдельно взятых слоев и можем получить общий модуль упругости всего основания целиком.

Оценка воздействия подвижного состава на путь

Оценка воздействия подвижного состава на путь по критериям прочности и надежности элементов верхнего строения.

Рассматриваемая оценка воздействия подвижного состава на путь по критериям прочности и надежности элементов ВСП является подразделом действующей в РЖД «Методики оценки воздействия подвижного состава на путь по условиям надежности» [103], вышедшего в дополнение к ЦПТ-52/14 [104].

В соответствии с [103], основной алгоритм расчетов пути на прочность основывается на следующих основных допущениях и предпосылках:

• рельс считается неразрезной балкой бесконечно большой длины неизменного сечения, лежащей на многих равноупругих точечных опорах или на сплошном равноупругом основании;
• вертикальные силы принимаются приложенными в плоскости симметрии рельсов. Рельсы обеих нитей колеи принимаются равнозагруженными;
• принимается, что колеса при движении не отрываются от рельсов и не создают ударных воздействий;
• в основе расчета лежит допущение о линейной зависимости между давлением на единицу площади основания и вызываемой им упругой осадкой основания;
• все характеристики пути, входящие в расчет, в том числе допускаемые напряжения, принимаются за неслучайные величины;
• при расчете рельса на изгиб за физическое допускаемое напряжение принимается минимально возможное значение условного предела текучести рельсовой стали;
• продольные температурные силы и силы угона непосредственно расчетом не учитываются, а учитываются только некоторым снижением физического допускаемого напряжения;
• горизонтальные поперечные силы и внецентренность приложения вертикальной нагрузки учитываются посредством специального коэффициента /0 перехода от осевых напряжений в подошве рельса к напряжениям в его наружной кромке;
• статическая нагрузка, передаваемая через колесо на рельс, принимается за неслучайную величину;
• воздействия переменных сил рассматриваются как статические;
• воздействия всех видов колебаний надрессорного строения учитываются эмпирически устанавливаемой величиной / дополнительного сжатия рессорного комплекта и динамической жесткостью рессоры;
• учитываются влияния изолированных неровностей на пути и изолированных и непрерывных неровностей на колесах;
• равнодействующая всех вертикальных сил, учитываемых расчетом и передаваемых расчетным колесом на рельс, берется в ее наибольшем значении с вероятностью Ф=0,994, что это значение не будет превышено;
• собственные напряжения в элементах верхнего строения не учитываются;
• расчет ведется для заданного сечения пути при движении по нему одноименных колес большого количества разных экипажей одного и того же типа. При этом расчетное сечение выбирают в месте наибольшего сжатия рессор.

Алгоритм определения критериев прочности для новых элементов ВСП основывается на кривой усталости Веллера (Рисунок 2.1).

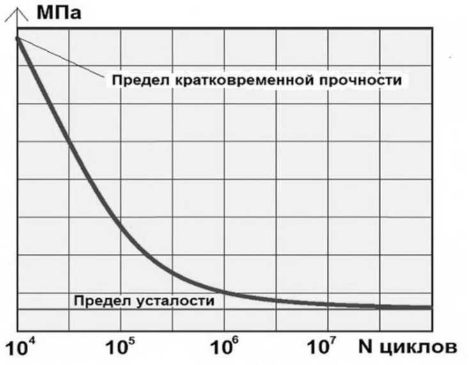
Рисунок 2.1 — Кривая Веллера для металлических материалов

Оценкой деформативности пути является модуль упругости пути и (МПа), который рассчитывается для всех современных конструкций пути. Основные расчётные формулы приняты в соответствии с [104, 105].

Оценка воздействия подвижного состава на путь по условиям обеспечения надёжности по [104].

Динамическая максимальная нагрузка на рельс:

Рд^^х=Р_ср + Л^ , кг (2.10)

• где Р_ср — среднее значение вертикальной нагрузки колеса на рельс, кг;
• 5 — среднее квадратическое отклонение динамической вертикальной нагрузки колеса на рельс, кг;
• Л — нормирующий множитель, определяющий вероятность события, т.е. появления максимальной динамической вертикальной нагрузки.

Среднее значение вертикальной нагрузки колеса на рельс:

Рср = Рст + Р_р^СР , кг (2.11)

• где Р_ст — статическая нагрузка колеса на рельс, кг;
• Рр^Р — среднее значение динамической нагрузки колеса на рельс от вертикальных колебаний надрессорного строения экипажа, кг.

Р_р^ср = 0,75Р_р^та% , кг (2.12)

• где Рр^па% — динамическая максимальная нагрузка колеса на рельс от вертикальных колебаний надрессорного строения экипажа, кг.

Р₁р^пах = кд(Рст — ч) , кг (2.13)

• где я — отнесённый к колесу вес необрессоренных частей, кг;
• кд — коэффициент динамических добавок от вертикальных колебаний надрессорного строения экипажа. Может быть получен экспериментальным путём, также рассчитывается:

кд = 0,1 + 0,2 у- Уст, (2.14)

• где V — скорость движения, км/ч;
• /ст — статический прогиб рессорного подвешивания, мм.

При расчёте рельса, как балки на сплошном упругом основании система сосредоточенных колесных нагрузок (Рисунок 2.2) заменяется эквивалентными одиночными нагрузками, соответственно при определении изгибающих моментов и напряжений в рельсах с помощью функции ц и при определении нагрузок и прогибов с помощью функции П- Поскольку в силу случайной природы вероятный максимум динамической нагрузки расчётного колеса не совпадает с вероятным максимумом нагрузок соседних колёс, то при определении эквивалентных нагрузок принимается максимальная вероятная нагрузка расчётного колеса и среднее значение нагрузок соседних колёс.

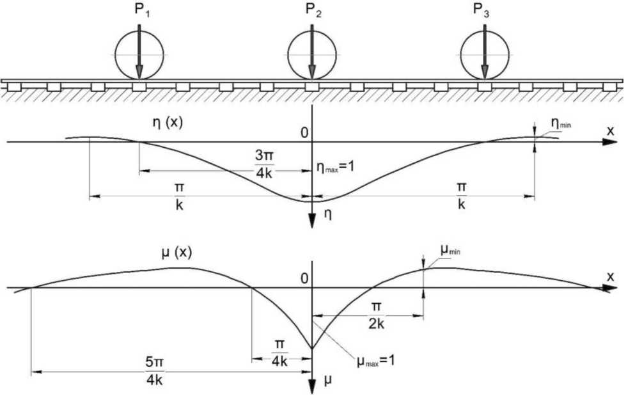
Рисунок 2.2 — Линии влияния прогибов и моментов от действия колёсной нагрузки

Максимальная эквивалентная нагрузка для расчётов напряжений в рельсах от изгиба и кручения определяется следующим образом:

РЭкв = РДИ^ I X «; Р_СР1 , кг (2.15)

• где » — ординаты линии влияния изгибающих моментов рельса в сечениях пути, расположенных под колёсными нагрузками от осей экипажа, смежных с расчётной осью.

Методика расчёта безбалластного пути как многослойной балки на упругом основании

Данная методика предполагает применение методологии прогнозирования ресурса безбалластных конструкций пути в реальных условиях эксплуатации, основанных на результатах испытаний БКП на Экспериментальном кольце АО «ВНИИЖТ», с использованием математического моделирования.

На основании предложенного сравнения безбалластного пути как многослойной балки, описанного А.Я. Коганом в ряде работ [106, 107, 108], предлагается следующая математическая модель.

В данной математической модели колебания пути рассматриваются как колебания конструкции, содержащей три бесконечно длинные балки, нижняя из которых лежит на модифицированном основании Винклера, а верхняя и средняя опираются на упругие прослойки, в основном имеющие характеристики основания Винклера. Для конкретной БКП (Рисунок 1.18) этими балками являются рельс, бетонная несущая плита (путевой бетон) и гидравлически связанный слой (тощий бетон).

На верхнюю балку действует переменная во времени динамическая нагрузка ^(^), движущаяся с постоянной скоростью у. Колебания данной системы описываются следующей системой дифференциальных уравнений в неподвижной системе координат [107].

При рассмотрении решения задачи в подвижной системе координат, перемещающейся вдоль оси х со скоростью у необходимо произвести замену и = х — у1, где и — абсцисса текущего сечения балки, отсчитываемая от начала координат, совмещенного с движущейся нагрузкой.

Данная математическая модель была верифицирована путем сравнения расчетных значений с результатами измерений напряжений и вертикальных прогибов слоев БКП. Прогибы и осадки ЩПГС и слоя полифилизированного грунта измерялись при помощи оптоволоконной системы диагностики земляного полотна [109, 110].

Зарубежные методы расчёта воздействия подвижного состава на железнодорожный путь

Метод Айзенманна

В основе данного метода лежит расчёт пути согласно гипотезы Фусса- Винклера, с дискретизацией точек опирания рельса, описанный в [111] и дополненный в [112].

В стандартном понимании классической конструкции железнодорожного пути расчёты пути на прочность ограничены квазистатическими нагрузками, в различных слоях пути, представленными в виде непрерывной балки на упругом основании. В таком случае к статическим нагрузкам добавляется динамическое приращение. Для элементарного расчёта пути, как балки на сплошном упругом основании принимается гипотеза Винклера [113], сформулированная в 1867 году, которая гласит, что сжимающее напряжение в каждой точке опоры пропорционально локальному сжатию. Данное отношение можно записать, как (Рисунок 2.3):

а = См, (2.31)

• где а — локальное сжимающее напряжение на опоре, Н/м²;
• IV — локальный прогиб опоры, м;
• С — модуль упругости основания, Н/м³.

При рассмотрении ситуации с дискретным опиранием рельса на подрельсовое основание, между вертикальной силой Р(Х[), воздействующую на опору Х[ с полезной площадью опирания А_Г5 и прогибом ш(Х[), существует следующая зависимость по Винклеру (Рисунок 2.4):

Р(хд = СА_Г5^(х₁) = к_а^(х^). (2.32)

В таком случае коэффициент жёсткости пружины равен:к_а = СА_ГЗ.

При рассмотрении системы, в которой рельс располагается на сплошном основании, между рельсом и основанием будет иметь место распределённая нагрузка, которая, по мнению Винклера, пропорциональна функции прогиба ш(х):

р(х) = кю(х~), (2.34)

• где к— коэффициент относительной жёсткости рельсового основания, который может быть рассмотрен, как коэффициент жесткости пружины на единицу длины Н/м/м.

В таком случае контактное давление на непрерывную рельсовую опору составляет:

о-_Г5(х) = р(х)Ь_с, (2.35)

• где Ъ_с — ширина опорной полосы под рельсом, м.

Конструкция, в которой рельс дискретно опирается на подрельсовое основание, может быть проанализирована численными методами. Однако для статической оценки и простых параметров может быть рассмотрена теория опирания рельса на сплошном основании (Рисунок 2.5) в качестве аппроксимации для конструкции с дискретными точками опирания. В таком случае эквивалентность следует из:

к » к_аа, (2.36)

где а — расстояния между осями дискретных точек опирания, м (Рисунок 2.4).При рассмотрении модели, где рельс представляется в виде бесконечно длинной балки (рельсовые плети бесстыкового пути) с изгибной жёсткостью Е1, которая поддерживается упругим основанием с коэффициентом основания к и нагружается колёсной нагрузкой ^ при х = 0. Данная расчётная модель балки впервые была предложена Циммерманном [114]

Исходя из необходимого условия равновесия элементов балки (Рисунок 2.7), определяется упругий прогиб балки IV (х). Поскольку в данной системе имеется только одна переменная х, то дифференциалы обозначаются буквенным значением й (а не 5).

Основным различием между расчётами для классического пути и безбалластного пути является значение коэффициента относительной жёсткости подрельсового основания к. Для шпального основания учитывается полезная площадь нижней постели шпалы и модуль деформации щебёночного балласта, а для безбалластной конструкции принимается в расчет жёсткость узла рельсового скрепления.

Функции ^(х) и //(х) определяют форму упругой линии и распределение моментов (Рисунок 2.8). Левая часть (х < 0) этих линий является результатом соображений симметрии. Эти линии могут также использоваться в качестве линий влияния для определения прогиба и изгибающего момента при х= 0, возникающих в результате воздействия соседних колёсных нагрузок. Эти выражения представляют собой сильно затухающие гармонические волны с длиной волны 2пк. Поэтому они также являются хорошим инструментом для аппроксимации конечных балок с центральной колесной нагрузкой при условии, что длина балки больше 2пк.

Принимая во внимание функции у(х) и р.(х) (2.43), имеется возможность рассчитать прогиб рельса у и изгибающий момент рельса М для цельного рельса (имеется ввиду без повреждений), изолированного стыка с поперечной силой сдвига 50%, а также произвести расчет для изломанного рельса [112] (Рисунок 2.9 и 2.10) . Влияние непосредственно самой балки (рельса) на прогиб или на момент вне точки приложения нагрузки может быть определено на основе графиков, линии прогиба и линии влияния момента инерции рельса.

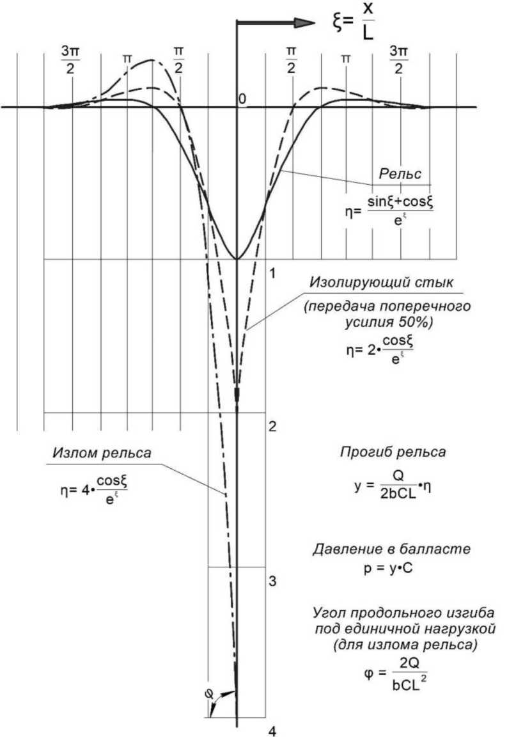
Рисунок 2.9 — Прогиб рельса у(х) по [112]

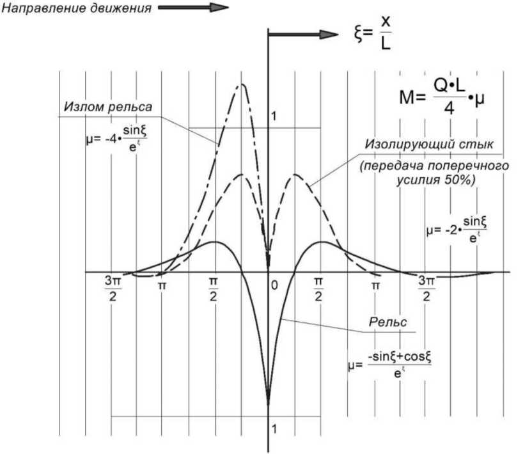
Рисунок 2.10 — Изгибающий момент рельса ^(%) по [112]

Самый наибольший негативный изгибающий момент при одноосном нагружении рельса происходит на расстоянии 0,5п^ от точки приложения нагрузки и составляет 21%, а при двухосном нагружении рельса на расстоянии п^ от точки приложения нагрузки и составляет 42% от позитивного крутящего момента под колесом. Это следует учитывать при исследовании усталостно-прочностных характеристик материала рельса с микротрещинами (Неад СИескз) на поверхности катания рельса. В изолированном стыке под воздействием катящегося колеса начинающийся перепад поверхности катания на линии прогиба рельса ведет к импульсному возмущению в комбинации с быстрым ухудшением положения пути на балласте [115]. При изломе рельса увеличивается негативный изгибающий момент на расстоянии 0,25п^ от места излома и составляет до 129% относительно позитивного крутящего момента рельса под колесом. Наибольший теоретический подъем рельса при одноосном нагружении происходит на расстоянии пЬ от точки приложения нагрузки и составляет 4%, а при двухосном нагружении на расстоянии 2пЬ от точки приложения нагрузки и составляет 8% от линии прогиба под осью колеса.

Подъем рельса, возникающий непосредственно в пути, бывает меньше или соответственно больше, чем теоретическое значение в зависимости от массы путевой решётки или в зависимости от негативного коэффициента модуля упругости безбалластного пути. При оценке стабильности классического балластного пути при повышении температуры рельсов в летний период следует принимать в расчёт снижение сопротивления поперечному сдвигу в районе подъёмной волны.

Метод АКЕМА

Метод описан в АКЕМА [119].Полная нагрузка на путь (статическая и динамическая) зависит от коэффициента динамического воздействия подвижного состава на путь.

Предлагаемые автором положения расчёта

В отечественной литературе параметр модуля упругости пути определяется как отношение упругого отпора основания пути к единице прогиба, в основе которой лежит модель Фусса-Винклера [113]. В таком случае рассматривается влияние каждого слоя рельсошпальной решётки на общий модуль упругости пути. При определении напряжении в рельсах от изгиба и кручения и напряжении в различных элементах подрельсового основания определяются две эквивалентные силы, принимаемые за нагружение расчётных точек. Данные модели позволяют определить расчётный изгибающий момент в рельсах, максимальную нагрузку на шпалу, максимальный прогиб рельса для условий классического пути. Согласно существующим методикам конструкция верхнего строения пути должна находиться в исправном состоянии. Значение модуля упругости пути и и коэффициента относительной жесткости рельсового основания и рельса к определялось экспериментальным путём комплексно, для заданных летних условий, без указания температурных диапазонов. В трудах В.П. Крачковского [122] подробно описано, что коэффициент относительной жесткости рельсового основания к зависит от модуля упругости пути и, который в свою очередь не является первичным и самостоятельным коэффициентом. Модуль упругости и представляет собой фиктивную силу, приходящуюся на 1 погонный см рельса и вызывающую его осадку на 1 см.

Модель сравнения базбалластного пути как многослойной балки, лежащей на модифицированном основании Фусса-Винклера, предложенная А.Я Коганом, требует сложных вычислений, вытекающих одно из другого, а также не учитывает влияние низких температур на упругие характеристики отдельных слоев.

Методы и методики, применяемые в отечественной практике, не позволяют в полной мере произвести расчёт требуемых параметров пути для БКП, а также не учитывают влияние температур на упругие характеристики элементов рельсовых скреплений.

В зарубежной практике расчётов пути на прочность в основе методов лежит также модель Фусса-Винклера [113] расчёта балки на сплошном упругом основании, дополненная Циммерманном [114]. Как в методе 8М’Т. так и в методе АКЕМА — основные силовые параметры пути определяются для классического балластного пути с рельсошпальной решёткой на железобетонных шпалах. В методе ЭВ в основе расчёта лежит модель Винклера-Циммерманна с дополнениями профессора Айзенманна [112, 123], который предполагает разделения на два этапа, аналогично предложениям В.П. Крачковского [124], и позволяет произвести вычисления для классического балластного пути, также и для БКП. Для вычисления прогиба рельса БКП вводятся известные первичные расчётные величины, что также аналогично предложениям В.П. Крачковского [122]. Но в данной модели, также как и в остальных моделях, не учитывается в расчётах влияние температур на упругие характеристики элементов и/или различных слоев пути.

На основе проведённого анализа выбрана в качестве расчётной модель для определения прогиба рельса БКП, предложенная и реализованная профессором Айзенманном [112].

Метод расчета упругого прогиба рельса БКП

Предлагается дополнить метод расчёта [112] формулой определения жёсткости узла рельсового скрепления с промежуточным эластичным слоем с введением температурных коэффициентов изменения статической и динамической жёсткости, определённых экспериментальным путём в лабораторных условиях.

Характеристическая длина, т.н. упруго работающая длина рельса для БКП, определяется по следующему уравнению:

Ь = (4^)0′^-5, (2.56)

• где Е — модуль упругости рельсовой стали, Н/мм²;
• I — момент инерции рельса, мм⁴;
• а — расстояние между осями дискретных точек опирания (промежуточных рельсовых скреплений), мм;
• с — модуль упругости дискретной точки опирания рельса (промежуточного рельсового скрепления), Н/мм.

В таком случае, прогиб рельса у в заданной точке, при нагружении рельса несколькими колёсными парами определяется исходя из требований уравнения, мм.

Для российских условий автор предлагает определять жёсткость узла рельсового скрепления, в состав которого входят два упругих элемента, как показано на Рисунке 2.11, исходя из взаимного влияния двух упругих элементов по аналогии с ГОСТ 34078 [99]. В таком случае жёсткость узла определяется по следующему равенству, Н/мм:

с = у ^Спр⁺ ^эп (2.60)

• где с_пр — жесткость подрельсовой прокладки;
• с_эп — жесткость эластичной прокладки.

В расчётах для рассматриваемого рельсового скрепления Система 300, вне зависимости от изменения температур, принимается постоянным значение статической и динамической жёсткости подрельсовой прокладки, выполненной из материала ЕVА 14%, со значениями 500 кН/мм и 1500 кН/мм соответственно.

В случае необходимости имеется возможность варьировать вводными параметрами подрельсовой прокладки, что отразится на конечном результате вычислений. Но как показывает статистика, влияние изменения жёсткости подрельсовой прокладки в данной системе рельсового скрепления не превышает 5%.

Рисунок 2.11 — Схематическое изображение прокладок в узле скрепления

С учётом влияния температур на упругие характеристики эластичной промежуточной прокладки в дискретной точке опирания рельса, статическая жёсткость эластичной прокладки определяется следующим образом, Н/мм.

В свою очередь динамическая жёсткость эластичной прокладки определяется с учётом формулы (2.61), Н/мм.

Принимая во внимание взаимовлияние близко расположенных друг к другу колёсных пар на прогиб рельса, автором построена расчётная модель воздействия на путь двух двухосных тележек, имитирующая сцепку двух вагонов, показанная на Рисунке 2.12.

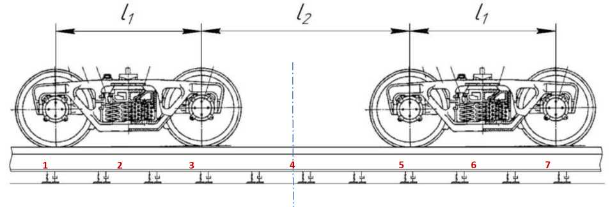
Рисунок 2.12 — Схема расположения тележек

Расчётная модель позволяет определить прогиб рельса как в статическом, так и в динамическом нагружении рельса от подвижных единиц. В расчёте (2.56) и (2.57), связанном с динамическим взаимодействием между БВСП и подвижным составом, учитывается коэффициент динамического усиления на модуль упругости дискретной точки опирания рельса, который определяется по следующему уравнению, согласно [2]:

к_ауп = 1 + 0-45ф, (2.63)

• где ^ — коэффициент влияния скоростей движения подвижного состава.

При скоростях движения менее 60 км/ч данный коэффициент принимается ^ = 1 вне зависимости типа движения, в других случаях определяется по следующим равенствам, согласно [2]:

для грузового движения при скоростях 60 < V < 140 км/ч:

<р = 1 + 0,5 • 5^р (2.64)

для пассажирского движения при скоростях 60 < V < 400 км/ч:

^ = 1 + 0,5 • 51900. (2.65)

Согласно [123] сила, возникающая в дискретной точке опирания рельса, определяется по следующему равенству, Н:

5 = с • у. (2.66)

Математическая модель позволяет произвести вычисления прогиба рельса БКП в заданной точке с учётом воздействия отрицательной температуры окружающей среды. Также имеется возможность варьировать входными параметрами, такими как:

• тип подвижного состава — грузовой или пассажирский;
• геометрические характеристики тележки вагона;
• осевая нагрузка;
• скорость движения;
• тип рельса;
• материал эластичной прокладки;
• номинальная статическая жёсткость эластичной прокладки;
• расстояние между узлами рельсовых скреплений;
• температура воздуха.

С целью проверки работоспособности расчётной модели были определены прогибы рельса БКП при статическом и динамическом нагружении от воздействия подвижного состава в диапазоне температур от -50 °С до +23 °С для грузового движения с осевой нагрузкой 250 кН со скоростью 70 км/ч, статической жесткостью эластичной прокладки 27,5 кН/мм, расстоянием между узлами скрепления 650 мм и рельсом типа Р65, расстояние 11=1850 мм, расстояние 12=3420 мм (Рисунок 2.13).

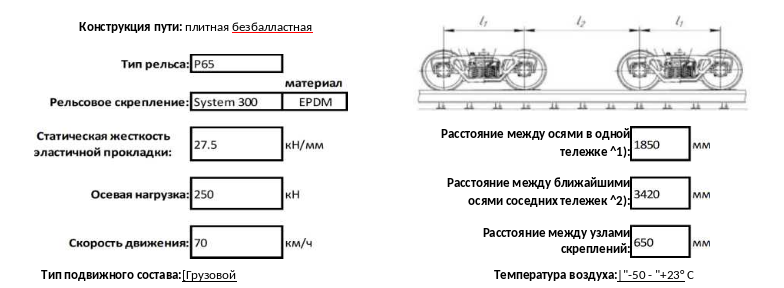
Результаты вычислений изменения прогиба рельса БКП от температуры узлов рельсового скрепления типа Система 300, для эластичных прокладок из двух материалов ЕР^М и Вуге1, представлены автором в виде графиков зависимостей на Рисунке 2.14.

Для автоматизации процессов вычисления адаптированная математическая модель реализована автором в виде макроса в Ехсе1 и в виде программного кода комплекса (Приложение А).

Выводы

1. Действующая на сети ОАО «РЖД» Методика оценки воздействия подвижного состава на путь по условиям обеспечения надёжности [103] в большей степени дублирует положения документа №ЦПТ-52/14 [104]. Основной акцент сделан на определении напряженно-деформированного состояния классической конструкции пути, для железобетонных или деревянных шпал. Значения модуля упругости пути и и коэффициента относительной жесткости рельсового основания и рельса к представлены в виде табличных данных для летних условий. Не предусматривается определение напряжённо- деформированного состояния БКП.
2. Методика, предложенная А.Я. Коганом, предполагает комплексную оценку безбалластной конструкции пути как многослойной системы, содержащей три бесконечной длины балки. Данная система не предполагает оценку воздействия температуры на отдельно взятую верхнюю балку, которая имитирует рельс.
3. Методы ЭВ, 8М’Т и АК.ЕМА рассматривают оценку напряжённого состояния рельсов в конструкции классического пути, состоящего из рельсошпальной решётки. Также не учитывается влияние температур на упругие характеристики отдельных элементов пути.
4. Метод Айзенманна предполагает определение упругого прогиба рельса для классической конструкции пути, состоящей из рельсошпальной решётки, а также для БКП. Расчетная модель учитывает предложения В.П. Крачковского об использовании первичных коэффициентов, влияющих на модуль упругости пути. Для безбалластной конструкции принимается в расчёт жёсткость узла рельсового скрепления, как главного элемента, формирующего упругие характеристики всей конструкции пути в целом. Отсутствует влияние температуры на изменение жёсткости узла рельсового скрепления.
5. Автор предлагает дополнить расчётную модель, указанную в методе Айзенманна, формулой определения жёсткости узла рельсового скрепления с эластичным слоем с введением коэффициентов влияния температуры на упругие характеристики элементов рельсового скрепления, полученных аппроксимацией зависимостей влияния низких температур на статическую и динамическую жёсткость эластичной прокладки рельсового скрепления, представленных в следующей главе.

Предложенная расчётная модель позволяет прогнозировать изменение прогиба рельса БКП с учетом влияния низких температур на жесткость узлов рельсовых скреплений в статическом и динамическом воздействии от подвижного состава.

Используемая Литература

• Методика оценки воздействия подвижного состава на путь по условиям обеспечения надежности. Утверждена Распоряжением ОАО «РЖД» №2706р от 22.12.2017, Москва, 2017.
• Лихтенберг, Б. Справочник «Железнодорожный путь». Нижнее строение — верхнее строение — текущее содержание — экономическая эффективность. — Гамбург: ЕигаПрге88, 20 1 0. — 432 с.
• Крачковский, В.П. Коэффициенты, применяемые при расчетах пути [Текст] / В.П. Крачковский // Труды МИИТа. — Вып. 54. — М.: Трансжелдориздат, 1937. — С. 125-213.
• Коган, А.Я. Колебания пути при высоких скоростях движения экипажей и ударном взаимодействии колеса и рельса [Текст] / А.Я. Коган, Д.А. Никитин, И.В. Полещук [и др.] // М.: Интекст, 2007.- 168 с.
• Коган, А.Я. Колебания пятислойной балки на упругом основании под действием подвижной динамической нагрузки [Текст] / А.Я. Коган, В.Ф. Барабошин, В.М. Гаврилов // Механика деформируемого тела и расчет транспортных сооружений: сб. науч. тр.: Новосибирск, 1986. — С. 33-43
• Коган, А. Я. Вертикальные динамические силы, действующие на путь [Текст] /А. Я. Коган // Тр. ВНИИЖТ. -1969. — Вып. 402. — 205 с.
• Методика оценки воздействия подвижного состава на путь по условиям обеспечения его надежности: №ЦПТ-52/14: утв. М.: ПТКБ ЦП МПС, 2000. 38 с.
• Правила производства расчетов верхнего строения железнодорожного пути на прочность / МПС СССР, ВНИИЖТ. — Москва. — 1954. — 60 с.
• Методика оценки воздействия подвижного состава на путь по условиям обеспечения надежности. Утверждена Распоряжением ОАО «РЖД» №2706р от 22.12.2017, Москва, 2017.
• Шахунянц Г.М. Железнодорожный путь: учебник для вузов ж.-д. трансп. [Текст] / Г.М. Шахунянц. — 3-е изд., перераб и доп. — М.: Транспорт, 1987. — 479 с.