Расчет и Проектирование Железобетонных Брусьев для Стрелочных Переводов

Схемы работы брусьев стрелочного перевода

На рис.2.1 представлены возможные схемы приложения силовых нагрузок Р/ и Р2 подвижного состава, передаваемых переводным брусьям, расположенным на разных участках (зонах) стрелочного перевода: стрелка, соединительные пути, крестовина, закрестовинные пути, переходные участки (зона перехода от стрелочного перевода к железобетонным шпалам). Во всех схемах на рис. 2.1 обозначены следующие размеры: 5 — расстояние между осями рельсов по прямому и боковому путям перевода, принимаемое во всех случаях одинаковым;

с — расстояние от оси крайнего рельса на брусе до конца бруса, принимаемое равным для прямого и бокового пути; Ь — длина бруса.

т и п — расстояние между точками приложения нагрузок при разных направлениях движения в разных зонах стрелочного перевода.

Для случая, показанного на рис. 2.1а, характерного для зоны стрелки, начала зоны соединительных путей и для переходных участков, величиной, определяющей конструкцию бруса, является

( = Ь-(3 + 2С) (2.1)

В зависимости от значения / возможны два варианта конструкции брусьев:

t < я/, где я/ — длина стрелочной подкладки, позволяющая объединить работу двух смежных рельсов, расположенных по прямому и боковому путям;

/ > лг/, если одной подкладкой нельзя объединить работу двух смежных рельсов и требуется установка двух раздельно расположенных подкладок.

При / = 0 — имеет место случай, характерный для брусьев на переходных участках и всех железобетонных шпал.

Для случая, показанного на рис. 2.16, характерного для конца зоны соединительных путей, крестовины и начала закрестовинных путей, величиной, определяющей конструкцию бруса, является

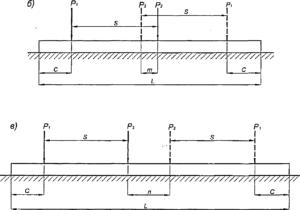
т = 2 (Б + С) —Ь (2.2)

Если значение т позволяет разместить на этом участке подкладку длиной Т, объединяющую работу рельсов по прямому и боковому путям, т.е. т < Т, то в средней части таких брусьев может быть выполнена общая площадка под такую подкладку.

Для случая, показанного на рис. 2.1 в, характерного для зоны закрестовинных путей, величиной, определяющей конструкцию бруса, является

п=Ь — 2(3+С) (2.3).

Рис. 2.1. Схемы передачи поездных нагрузок на переводные брусья Б, С, 1-, I, ш, п — параметры точек приложения нагрузок на брус

Если значение п < Т, то в средней части бруса следует размещать площадку для общей подкладки длиной Т. Если п > Т, то в середине бруса следует размещать две площадки под одиночные рельсовые подкладки длиной а/.

Исходя из приведенных выше возможных схем передачи силовых нагрузок и соответствующих им требованиям к конструкции брусьев, предложены 4 типа схем железобетонных брусьев, представленные на рис. 2.2.

На схемах показано, что передача нагрузок на брусья производится не в виде сосредоточенных сил, а в виде нагрузки, распределенной по длине подкладок, включая прокладки. Подкладки заглубляются в брусья на величину к_а для передачи поперечных сил на бетон.

Схема I соответствует случаю передачи нагрузок на брус, показанному на рис. 2.1а, при / < Д/;

Схема II соответствует тому же случаю, но при / > а

Схема III соответствует случаю нагружения, показанному на рис. 2.16, при т < Г;

Схема IV соответствует нагружению, показанному на рис. 2.1 в, при п > 2а\.

Основными геометрическими параметрами, определяющими конструкцию брусьев, показанными на рис. 2.2, являются:

• А — расстояние по оси бруса между наружными кромками углублений в подрельсовых площадках, принадлежащих одной рельсовой колее;
• В — расстояние по оси бруса между наружными кромками углублений в крайних подрельсовых площадках на разных концах бруса;
• Є — расстояние по оси бруса от наружной кромки углубления в крайней подрельсовой площадке на одном (обычно — левом) конце бруса до ближнего к нему кромки углубления в средней части бруса;
• а/ — расстояние по оси бруса между кромками одного углубления подрельсовой площадке, расположенной в концевой части бруса;

Все эти параметры задаются проектом стрелочного перевода для каждого бруса в зависимости от типа, марки перевода и принятой конструкции прикрепления рельсов и стрелочных переводов.

Все остальные размеры брусьев не задаются, а являются объектом расчета и проектирования брусьев.

Участки бруса между заглубленными площадками для стрелочных и рельсовых подкладок могут иметь либо постоянную, либо и переменную по длине бруса высоту, см. рис.2.2.

Если расстояние между подрельсовыми площадками достаточно велико, то между ними целесообразно устраивать участки с меньшей высотой бруса, положительное значение которых подробно освещено ниже в разделе 2.5 настоящей работы.

Схемы брусьев определяют размещение на них подрельсовых площадок.

Для определения силовых факторов (изгибающих моментов), возникающих в брусьях при их работе в пути под поездной нагрузкой и необходимых для разработки конструкции брусьев, на рис.2.3 представлены расчетные схемы для всех типов брусьев.

Эти схемы предусматривают:

• конструкцию бруса, симметричную относительно его середины;
• одностороннее относительно середины бруса приложение расчетных вертикальных нагрузок в точках опирания рельсов;
• равномерное опирание бруса по всей длине на сплошное упругое основание (по Винклеру) с постоянным показателем упругости;
• одинаковую ширину бруса понизу по всей длине.

Переменными величинами в расчетных схемах для разных типов брусьев являются:

• длина бруса;
• расстояния точек приложения нагрузок Р/ и Р₂ от концов бруса; высота бруса на разных его участках;

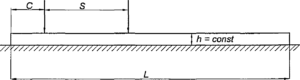
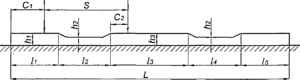
а)

б) Рис. 2.3. Расчетные схемы брусьев с постоянным по длине (а) и переменным (б) поперечными сечения мидлина участков с разной высотой и расстояния границ участков от точек приложения нагрузок.

Для брусьев с высотой постоянной, по всей длине, расчетная схема имеет вид, показанный на рис. 2.3, а для брусьев с переменной высотой на рис. 2.36.

Расчетные нагрузки на брусья

Действие поездных нагрузок на брусья представлено в виде сосредоточенных вертикальных сил Р₁ и приложенных по середине тех подрельсовых площадок бруса, на которые передается нагрузка от колес подвижного состава при проходе его по переводу в данном направлении. При движении поезда по другому направлению точки приложения сил Р\ и 7^ на брусе соответственно меняются.

Значения нагрузок Р\ и Р? в каждой зоне перевода для возможности расчета конструкций брусьев взяты на основании результатов теоретических и экспериментальных исследований, выполненных в стрелочной лаборатории отделения пути ВНИИЖТ [49].

В пределах зоны стрелки нагрузки Ру и Р2 на концы бруса различны, что обусловлено разницей в распределяющей способности остряка и рамного рельса, а также наличием динамической добавки сил при перекатывании колеса с остряка на рамный рельс (или наоборот).

Рамный рельс передаваемую на него колесную нагрузку распределяет на несколько брусьев. Нагрузка на один конец бруса Р₁ в месте опирания на него подкладки рамного рельса может быть принята такой же, как и нагрузка на шпалу Р_ш, и определена по известной формуле [53].

Р_ш=\Ро_ин, (2.4)

где к — коэффициент относительной жесткости подрельсового основания и рельса;

/ — расстояние между осями железобетонных шпал или брусьев;

Р_дин — динамическая нагрузка колеса на рельс.

Остряк стрелки, в силу своей гибкости отсутствия иной связи со стрелочным башмаком кроме опирания на него, передает колесную нагрузку более сосредоточенно. В неблагоприятном случае, при наличии неработающих брусьев рядом с расчетным брусом, как показали путевые испытания, нагрузка на брус непосредственно под остряком может достигать до 80% всей нагрузки колеса на рельс Р_дин. Поэтому расчетная нагрузка на другой конец бруса Р2 в зоне стрелки может быть принята 0,8 Р_дин [49].

В зоне соединительных путей также имеется разница в величине нагрузок на разные концы бруса при движении состава по прямому и по боковому направлениям. На основании путевых испытаний [49], для прямого направления в большинстве случаев Р₁ = Р2 = Р_Ш. Для бокового пути в кривой, в связи с перераспределением нагрузок на внутренний и наружный рельсы, величина /Сможет составлять до Р2 = 2Р. Поэтому при уменьшенном значении Р1 для всех брусьев, расположенных в зоне соединительных путей, были приняты следующие расчетные нагрузки:

где Р_ш— значение, определенное по формуле (2.4). В зоне крестовинного узла величина нагрузки Р1 на брус под рельсом, соединенным с контррельсом, может быть определена по формуле аналогичной формуле (2.5) как Р_х = — Р_ш.

Величина нагрузки Р2 на брус непосредственно под крестовиной определяется по формуле: ^ ^с — ^ ‘

Л^^+ДО, (2.6)

где А/ — коэффициент относительной жесткости подрельсового основания и крестовины, учитывающий, что момент инерции крестовины в среднем в два раза больше момента инерции рельса;

Статическая нагрузка на крестовину от колеса подвижного состава;

ДРдип — динамическая добавка нагрузки на крестовину при перекатывании колеса с усовика на сердечник крестовины и обратно.

Величина ЛР_дШ1 зависит от целого ряда факторов, таких как масса крестовины, жесткость упругих прокладок под крестовиной, траектории перекатывания колеса по крестовине и многих других.

На основании экспериментальных данных [49] в расчетах величина ЛР_дин принималась равной 320 кН.

В зоне путей за крестовиной нагрузки Р/ и Р₂, возникающие от действия подвижного состава, могут быть приняты аналогичными действующим в обычном пути с железобетонными шпалами. При расчете железобетонных шпал обычно принимают

Р1 = Р₂ = Р_Ш, (2.7)

где Р_ш — максимальная вероятная нагрузка на шпалу для данных условий пути и подвижного состава. Учитывая, однако, что перегрузка внутреннего рельса создает более сложные условия работы длинного бруса (возрастает положительный момент под рельсами), для расчетов брусьев использованы формулы, учитывающие перегрузку одного из рельсов.

Выполненные ЦНИИ МПС ранее [11] испытания показали, что если на один конец железобетонной шпалы действует максимальная вертикальная нагрузка Р_ш, то наиболее вероятно, что на другом конце этой шпалы нагрузка составляет примерно 0,75 Р_ш. С учетом этого были приняты следующие расчетные нагрузки на брусья для закрестовинного участка:

Р1⁼ 0»75 Р_ш и Р₂= Р_ш (2.8)

Брусья переходного звена (с переменной подуклонкой подрельсовых площадок) и брусья типа ПЛ (без подуклонки подрельсовых площадок) работают примерно так, как обычные железобетонные шпалы, и для них по аналогии были приняты расчетные нагрузки как при симметричном загружении

— Р, = Р₂=Рш.

Расчет брусьев на прочность и трещиностойкость проводится от действия вертикальных сил. Горизонтальные силы, имеющие важное значение для расчета скреплений и других металлических деталей стрелочного перевода, а также для оценки его эксплуатационных качеств в целом, как показал опыт расчета и проектирования железобетонных шпал [72], мало влияют на работу элементов подрельсового основания.

Величина сил Р_ш, действующих на железобетонные шпалы при различных характеристиках пути и подвижного состава, определяется в соответствии с «Методикой оценки воздействия подвижного состава на путь по условиям обеспечения его надежности», разработанной ВНИИЖТом и утвержденной МПС [53].

На рис 2.4 представлены схемы расчетных нагрузок, действующих на брусья в разных зонах стрелочного перевода.

Расчет железобетонных брусьев для стрелочных переводов

Железобетонные шпалы обычно рассчитывают как балки конечной длины на упругом основании (по Винклеру), реакция которого (<7) пропорциональна величине прогиба (у) балки:

Ч = Су, (2.9)

где С — так называемый «коэффициент постели», характеризующий упругие свойства основания.

Этот метод расчета, как и всякий другой имеет условности и допущения, в той или иной мере схематизирующие действительное взаимодействие балки с основанием. Одной из таких условностей является принятие упругой связи с основанием не только при прогибе балки вниз, но и при выгибе ее вверх, что в действительности обычно отсутствует. Как показали многочисленные испытания железобетонных шпал в лабораторных условиях на специальных установках, воспроизводивших работу шпал в пути [71,72], достаточно близкая сходимость расчетных результатов с экспериментальными наблюдается, если изгиб балки происходит в зоне ее положительных прогибов и отрыв балки от основания отсутствует. При этом случае были получены близкие результаты

Рис. 2.4. Расчетные нагрузки на брусья разных зон стрелочного перевода: а-стрелка; б-соединительные пути; в-крестовина; г-закрестовинные пути; д -переходные участкисравнения значений напряжений и прогибов, полученных расчетом и непосредственно измеряемых.

Такое соответствие наблюдается при испытании сравнительно коротких балок (или их отдельных участков), когда соотношение Л=— между длиной (/,) балки (или ее участка) и характеристикой относительной жесткости основания и балки (5), измеряемой в единицах длины, находится в пределах от 0,5 до 2,5, где (2.10)

• Е — модуль упругости материала балки, кг/см ,
• J — момент инерции сечения балки, см⁴,
• Ь — ширина балки понизу, (см),
• С — коэффициент постели основания кг/см³.

К таким коротким балкам относятся железобетонные шпалы или отдельные участки длины этих шпал (подрельсовых частей и средней части при постоянном поперечном сечении этих участков).

Для переводных брусьев, имеющих значительно большую длину, чем шпалы, указанное выше условие обычно не выполняется.

Расчет шпал как балок конечной длины на упругом основании выполняют обычно с использованием метода начальных условий [74], по которому все силовые и геометрические факторы в сечениях по длине балки выражают через такие же факторы в ее начале. Расчет по этому методу балок, имеющих постоянное поперечное сечение по длине, прост, удобен и дает, как указано выше, приемлемую сходимость с результатами испытаний. Следует, однако, отметить, что все расчеты требуют надежного обеспечения вычислительной техникой, особенно с увеличением длины балок.

Одним из вопросов настоящей работы является исследование целесообразности применения брусьев не с постоянным, а со ступенчатым изменением поперечного сечения по длине бруса. Расчет балок с переменным поперечным сечением по методу начальных условий резко увеличивает трудоемкость, т.к. при каждом изменении сечения возникает необходимость расчета новой балки с новыми начальными условиями, определяемыми только на последнем этапе вычислений. Снижается точность и достоверность расчетов. Поэтому методика расчета балок на упругом основании по методу начальных параметров не целесообразна для расчета переводных брусьев с переменным поперечным сечением

Для решения поставленной задачи в настоящей работе был применен другой способ расчета балок на том же упругом основании с гипотезой коэффициента постели, но без применения метода начальных условий, а с использованием метода сечений, применяемого в строительной механике.

Способ расчета балок на упругом основании с использованием метода сечений был детально разработан A.M. Овечкиным [57]. Для расчета путевых конструкций этот метод не применялся, хотя для сложных конструкций с переменным поперечным сечением он очень эффективен.

По этому методу балка любой длины с постоянным или переменным сечением по длине, с различными условиями опирания, симметричным или несимметричным загружением внешними силами в любых точках балки, может быть представлена в виде системы многих элементарных балочек, связанных между собой внутренними изгибающими моментами и поперечными силами, отражающими фактическую неразрывность всей балки (рис. 2.5).

Каждая элементарная балочка имеет постоянное по ее длине поперечное сечение, упругое основание с неизменным коэффициентом постели и рассчитана на действие одного изгибающего момента (М) и одной поперечной силы (Q или Р), приложенных на конце балки.

Применяя этот метод для расчета переводного бруса мысленно разрезают брус в местах приложения внешних вертикальных сил Р₁ к Р₂ ив местах изменения поперечного сечения на ряд элементарных балочек (см. рис. 2.5). В местах разрезов прикладывают внутренние изгибающие моменты М/ и поперечные силы Qj, взаимно уравновешивающие друг друга.

Таким образом, расчет длинного бруса с переменным поперечным сечением сводится к расчету системы коротких простых балочек, достоверность расчетов которых уже проверена ранее.

Пользуясь методом сил по правилам строительной механики, составляют систему канонических уравнений.

Для бруса, показанного на рис.2.5, б, (зона соединительных или закрестовинных путей), система будет состоять из 12 аналогичных канонических уравнений.

В системах уравнений приняты следующие обозначения: А], и Д» — перемещения концов левой и правой балочек в месте разреза под действием изгибающего момента М,- по направлению действия этого же момента; индекс / в соответствии с рис.2.5 может принимать нечетные значения — 1, 3, 5 и т.д.; Д-; И А»^- такие же перемещения, НО ПОД действием поперечной СИЛЫ 12; или (Р-01) по направлению действия этой силы; индекс } может принимать четные значения — 2, 4, 6 и т. д.; Д’_;и или А), и А], — перемещения концов левой и правой балочек в месте разреза под действиями момента М₁ и силы Qj по направлению или против направления (знак минус) всех прочих усилий.

Для балки по рис. 2.5а, а матрица коэффициентов при неизвестных дана в табл. 2.1.

(2.11) Перемещения определяются по формулам, представленным в табл.2.2 [57], в зависимости от категории балочки.

Для решения системы канонических уравнений был использован метод Гаусса, суть которого состоит в том, что система уравнений путем последовательного исключения неизвестных приводится к системе с треугольной матрицей, из которой затем определяются значения неизвестных М; И О,.

Зная значения М[ и Q[ для начала каждой элементарной балочки, можно, при необходимости, найти все характеристики напряженно- деформированного состояние этой балочки в любом ее месте по длине: изгибающий момент — М^ поперечную силу — 0,_ч

По этой методике была составлена программа для ПК и произведен расчет всех брусьев стрелочных переводов.

Практически для расчета и конструирования брусьев нет необходимости определять все эти значения. Для разработки конструкции бруса достаточно знать только наибольшие значения М и Qb его расчетных сечениях, которыми обычно являются сечения в точках приложения сил P¡ И Р2 и по середине участков между ними, особенно при меньшей их высоте.

Значения изгибающих моментов в точках приложения нагрузок получаются прямо из результатов расчета, так как в этих сечениях принимается граница участков, а значение момента по середине участка между P¡ и Р2 определяют по формуле А/0,5 для жесткой балки (2.13).

Расчет брусьев с переменным поперечным сечением производят в следующем порядке:

1. Для каждого бруса в зависимости от положения его в стрелочном переводе заданного типа и марки принимают схему и основные геометрические параметры бруса (см. рис. 2.2) и определяют вертикальные нагрузки P¡ и Р2, действующие на брус (см. п. 2.2). Значения нагрузок вводят в программу ПК.
2. Разбивают брус на элементарные балочки в соответствии с принципами, изложенными ранее. Для каждой балочки задают длину, размеры поперечного сечения, его момент инерции, коэффициент постели основания. Все параметры элементарных балочек вводят в ПК.
3. В результате расчета по программе получают значения изгибающего момента в расчетных сечениях бруса: в точках приложения сил Р/ и Р2 и по середине участков между ними. Наибольшие значения этого момента при изгибе бруса вниз (положительное направление момента) и вверх (отрицательное направление момента) принимают для расчета конструкции бруса, как на конкретном участке — длине балочки, так и бруса в целом. При необходимости по формулам (2.13) — (2.16) могут быть вычислены и построены полные эпюры моментов для всего бруса.
4. Полученные значения положительного изгибающего момента в пределах подрельсовых площадок корректируют с учетом распределения сосредоточенных вертикальных нагрузок и Р2 подкладками скреплений в соответствии с п. 2.4 (см. ниже).
5. По полученным значениям расчетного изгибающего момента, возникающего в данном сечении бруса в эксплуатации (М_э), определяют требования, которым должно это сечение удовлетворять по условиям трещиностойкости — отсутствия образования трещин при эксплуатационной нагрузке.

По действующим строительным нормам и правилам расчета железобетонных конструкций [77] предельный момент по трещиностойкости сечения {Мщ) определяется в общем виде по формуле:

м_тр= IV(Оз.р. + <Т_д._ст), (2.16)

где IV- момент сопротивления поперечного сечения бруса,

<У₆.р. — прочность бетона на растяжение,

СТб.ст — предварительное обжатие бетона, расположенного в растянутой зоне сечения, предварительно напряженной арматурой.

Расчетная прочность бетона на растяжение — величина постоянная для данного класса бетона и по величине незначительная (например для бетона класса В40-21 кг/см²).

Величина Сб.ст для каждого сечения различна и определяется формулой,

где N — сила предварительного натяжения арматуры, Г — площадь поперечного сечения, IV — момент сопротивления поперечного сечения, е — эксцентриситет приложения центра тяжести напряженной арматуры относительно центра тяжести сечения.

Если полученное расчетом значение М₃ меньше предельного значения М_тр для первоначально принятого сечения бруса М_э< Мтр, то трещиностойкость конструкции с тем или иным запасом обеспечивается.

Если М₃> М_тр, то необходимо внесение в конструкцию бруса изменения, руководствуясь формулой (2.18) соответственно изменяя размеры сечения, количество, силу натяжения и расположение напряженной арматуры.

Распределение нагрузки на брус подкладками рельсовых скреплений

Изложенная методика предполагает передачу нагрузок на брус в виде сосредоточенных сил. Однако фактически нажатие рельса на брус передается в виде распределенной по некоторому закону нагрузки, поэтому острых пиков изгибающего момента в точках приложения вертикальных сил на самом деле нет. Это подтвердили как теоретические исследования, так и специально поставленные опыты с железобетонными шпалами [72]. Было установлено, что фактические значения расчетного изгибающего момента в подрельсовых зонах переводных брусьев меньше полученных при сосредоточенном действии сил.

При расчете железобетонных шпал считают вертикальную нагрузку на шпалу равномерно распределенной на уровне нейтральной оси подрельсовой части шпалы на участке длиной /.

/=Ь_лод + 2(Ь_ш+Ь_п^30^о, (2.17)

где Ъ_под — ширина подошвы рельсов; И_ш — расстояние от нейтральной оси до верха шпалы в подрельсовом сечении; И„ — суммарная высота подкладки (если она имеется) и прокладок под рельсом; 30° — угол, под которым, как условно предполагают, распределяется давление внутри шпалы.

Такой же способ распределения вертикальной нагрузки можно было бы принять и при расчете железобетонных брусьев стрелочных переводов, но опыт расчета брусьев со ступенчатым изменением поперечного сечения по методике, изложенной в п. 2.3, показал, что замена сосредоточенных сил Р/ и Р₂ распределенными нагрузками приводит к значительному усложнению вычислений. Поэтому во всех случаях расчета применять сосредоточенные вертикальные силы Р₁ и Р₂, а распределяющее действие подкладок учитывать введением «коэффициента распределения» (к^ к полученным значениям изгибающего момента, при сосредоточенной нагрузке.

Величина коэффициента к_п была получена серией расчетов при разных значениях длины распределения / по формуле (2.17). Результаты представлены на рис.2.6, 2.7 и в табл. 2.3.

В зоне соединительных путей, на участках за крестовиной, на брусьях типа ПЛ и переходного звена, где конструкция подкладок на брусьях не отличается от применяемых для шпал, длину участка передачи вертикальной нагрузки на брус следует определять непосредственно по формуле (2.17). Для брусьев расположенных в зоне стрелки, длину участка распределения / вычисляли по формуле (2.17), но в ней вместо ширины подошвы рельса следует принимать длину стрелочной подушки. Для брусьев, расположенных в зоне крестовинного узла, длину / также следует принимать по формуле (2.17), но вместо ширины подошвы рельсов учитывать ширину крестовины понизу.

Изложенные в настоящей главе методы расчета и проектирования железобетонных брусьев для стрелочных переводов приняты к использованию специалистами отдела «Конструкции железнодорожного пути» ФГУП ВНИИЖТ при разработке новых конструкций переводных брусьев для всех типов стрелочных переводов. В Приложении 1 к настоящей работе дан перечень проектов брусьев, разработанных за последние годы. Проекты утверждены Департаментом пути и сооружений МПС России. Большинство разработанных брусьев уложено на дорогах России для серийного или опытного применения.

В результате анализа ежегодных отчетных материалов специализированных организаций МПС, осуществляющих наблюдения за стрелочными переводами с железобетонными брусьями, установлено отсутствие выхода или замены брусьев по дефектам или повреждениям, связанным с их недостаточной прочностью.

Отдельными комиссионными обследованиями железобетонных брусьев новых опытных стрелочных переводов были отмечено появление микротрещин в бетоне брусьев на участках между подрельсовыми площадками, где по условиям расположения рельсовых и стрелочных подкладок не было выполнено переменное сечение с углублением в бетон.

Так, например, при обследовании стрелочных переводов типа 2750 с железобетонными брусьями на ст. Калачинская Западно-Сибирской ж. д., выполненное по распоряжению МПС С-4284 от 06.05.99. были отмечены микротрещины в брусьях №29-60. В приказе МПС по результатам этого обследования разработано указание «В железобетонных брусьях с целью повышения их трещиностойкости ввести выемки в средней части, где это возможно конструктивно, а также по условиям производства и работы обслуживающего персонала». Тем самым была подтверждена эффективность устройства переменного по высоте поперечного сечения переводных брусьев, что явилось практическим подтверждением результатов правильности исследований, изложенных в настоящей главе.

Выводы

1. Разработанная в результате настоящих исследований методика расчета железобетонных брусьев с переменным по длине поперечным сечением позволяет решать вопросы обеспечения прочности и трещиностойкости железобетонного подрельсового основания стрелочного перевода.
2. Расчет переводных брусьев методом сечений, позволяющий приводить расчет длинного бруса к системе отдельных коротких балок с постоянным поперечным сечением, достоверность результатов расчета которых уже проверялось ранее при испытаниях железобетонных шпал.
3. Железобетонные брусья по своей конструкции и условиям работы в разных зонах стрелочного перевода могут быть приведены к четырем типовым схемам, представленным в настоящей работе и включенным в первый отечественный стандарт ОСТ 32.134-99 на эти брусья.
4. При работе брусьев в стрелочном переводе под поездной нагрузкой на участках брусьев между подрельсовыми площадками возникает значительный изгибающий момент отрицательного направления (изгиб бруса вверх), величина которого достигает до 40-50% от наибольшего расчетного момента (изгиб бруса вниз) в местах подрельсовых площадках.
5. Для обеспечения трещиностойкости брусьев наиболее целесообразным техническим решением является применение брусьев с переменным по длине поперечным сечением, в частности, с уменьшенной высотой бруса на участках между подрельсовыми площадками, что достигается устройством местных углублений в бетоне на этих брусьях.
6. Для конкретных брусьев уменьшение на 30% высоты поперечного сечения бруса на участках между подрельсовыми площадками снижает величину изгибающего момента отрицательного направления на 20-30% и является эффективным средством обеспечения трещиностойкости этих участков.
7. При уменьшении высоты поперечного сечения бруса достигается возможность повышения предварительного обжатия бетона напряженной арматурой без увеличения ее количества и соответственно повышения трещиностойкости сечения при экономии бетона.

Используемая литература

53. Министерство путей сообщения Департамент пути и сооружений. «Методика оценки воздействия подвижного состава на путь по условиям обеспечения его надежности». ЦПТ-52/14
54. Крысанов Л.Г. Конструкция элементов основания стрелочных переводов. — В кн.: Железобетонные шпалы для рельсового пути. Под ред. А.Ф. Золотарского. М. Транспорт. 1980. С. 144-184.
55. Вериго М.Ф. Основные положения методики расчета сил, действующих на железобетонные шпалы. — В кн. Усовершенствование железобетонных шпал. Труды ВНИИЖТ, вып. 257. М. 1963. С. 5-39.
56. Серебренников В.В. Исследование работы струнобетонных шпал: дисс. канд. техн. наук. Защ.21.11.54; ВНИИЖТ. 1953. 258 с.
57. Серебренников В.В. Расчет железобетонных шпал. В кн. Железнодорожный путь на железобетонных шпалах. Под ред. А.Ф. Золотарского. М. Транспорт. 1967. С. 131-183.