Цикл статей:
Глава 1 — Совершенствование технологии эксплуатации грузовых вагонов с инновационными тележками
Глава 2 — Сравнительный анализ динамических качеств грузовых вагонов с разными типами тележек
Глава 3 — Исследование динамической нагруженности грузовых вагонов с нелинейным рессорным подвешиванием ходовой части в системе «вагон-путь»
Глава 4 — Технология эксплуатации грузовых вагонов с инновационными тележками по гарантийным участкам повышенной протяженности
Аналитическое представление силовой характеристики тележки
рессорного подвешивания Barber
Для исследования динамики подвижного состава применяются несколько математических моделей железнодорожного пути разной степени сложности и детализации процессов, протекающих в нем. Во многих случаях применяется модель абсолютно жесткого пути, т.е. путь описывается только геометрическими неровностями, а также неровностями на поверхности катания рельсов. Как показывает практика исследований, погрешность такой идеализации железнодорожного пути можно оценить в 10-15%, что вполне удовлетворительно с инженерной точки зрения [34].
Обоснование данной идеализации подтверждается результатами многочисленных исследований, позволивших идентифицировать параметры железнодорожного пути и спектральную плотность геометрической неровности на основании эмпирических данных [2; 40]. В результате оказалось, что колесная пара практически в точности повторяла геометрическую неровность пути при ее безотрывном движении по рельсам, следовательно, можно понизить число степеней свободы подвижного состава.
Существенным отличием новых инновационных вагонов, выпускаемых Тихвинским вагоностроительным заводом, оснащенных тележками Barber, и вагонов производства Уральского вагоностроительного завода с тележками модели 18-194-1 от вагонов старых моделей с тележкой 18-100 является то, что тележки Barber и 18-194-1 имеют нелинейное рессорное подвешивание, способствующее повышению безопасности движения вагонов в порожнем режиме их движения [60].
Как уже было показано выше, силовая характеристика рессорного подвешивания такой тележки, представленная на рисунке 2.1 , имеет переломы, соответствующие прогибам 0-0,005; 0,005-0,015; 0,015-0,050 и свыше 0,050 м.
Таким образом, рессорное подвешивание новых тележек грузовых вагонов обладает кусочно-линейной силовой характеристикой. При возможном наличии неровностей пути с большой амплитудой [71], вызывающей интенсивные колебания вагона с соответствующими большими динамическими прогибами рессорных комплектов, превышающими диапазоны отдельных участков силовой характеристики, для дальнейших исследований необходимо получить ее аналитическое представление, так как решение задачи методами качественного исследования, в данном случае методом припасовывания, чрезвычайно трудоемко. Аналитическое представление силовой характеристики возможно получить следующим образом.
Сначала с использованием эмпирического материала строится сплайн- преобразование, которое состоит из минимально необходимого числа кубических парабол, число которых определяется выбираемой нами точностью представления исходных данных.
С помощью известного метода наименьших квадратов, причем суммы были заменены на интегралы, которые необходимо было вычислять с заданной точностью, вначале находим сплайн-преобразование силовой характеристики рессорного комплекта, строим кубический полином для одного рессорного комплекта подвешивания кузова вагона:

Нужно отметить, что эти коэффициенты зависят от диапазона, на котором определена силовая характеристика рессорного подвешивания экипажа. Ниже на рисунке 3.1 показаны эмпирическая и аппроксимирующая силовые характеристики кривые. Кубический полином хорошо описывает исходную кусочно-линейную кривую. Некоторые отличия обнаруживаются в точках перелома и в начале координат, что некритично, потому что колебания подпрыгивания кузова вагона происходят относительно положения, достаточно близкого к статическому равновесию.
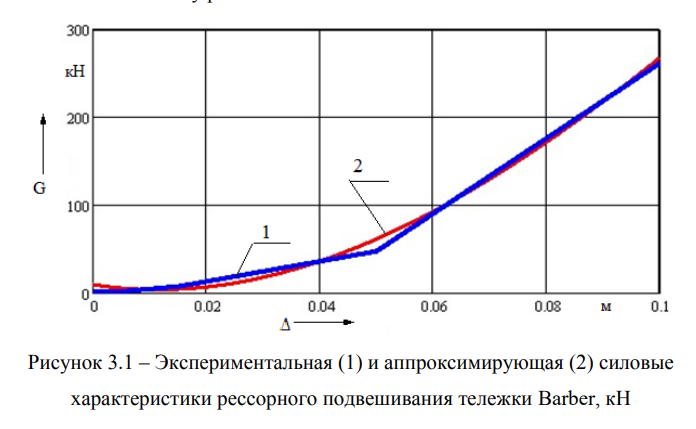
Из теории колебаний известно, что жесткость любой силовой характеристики есть производная от силовой характеристики по прогибу.
Определим ее для рессорного подвешивания (рессорного комплекта) вагона, взяв производную от силовой характеристики по прогибу:
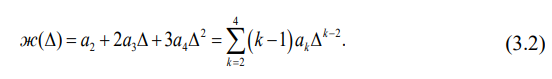
Ниже на рисунке 3.2 показан график жёсткости нелинейного рессорного подвешивания кузова вагона на тележках Barber как функции прогиба. Здесь заметим, что, вследствие полученной аппроксимации кусочно-линейной силовой характеристики кубическим полиномом значение жесткости при прогибах до 7 мм является отрицательным, что, разумеется, противоречит физическому смыслу. Этот факт можно не принимать во внимание, так как величины статических прогибов рессорного комплекта как в порожнем режиме, так и в груженом режиме незначительные — нам необходимо оценить динамические свойства вагона прежде всего в порожнем режиме, так как в груженом режиме движения вагона они в несколько раз больше. Как видно из рисунка 3.2, в груженом состоянии кузова при его вертикальных колебаниях около статического равновесия, расчетная и экспериментальная характеристики близки друг к другу, поэтому такая аппроксимация является вполне допустимой.
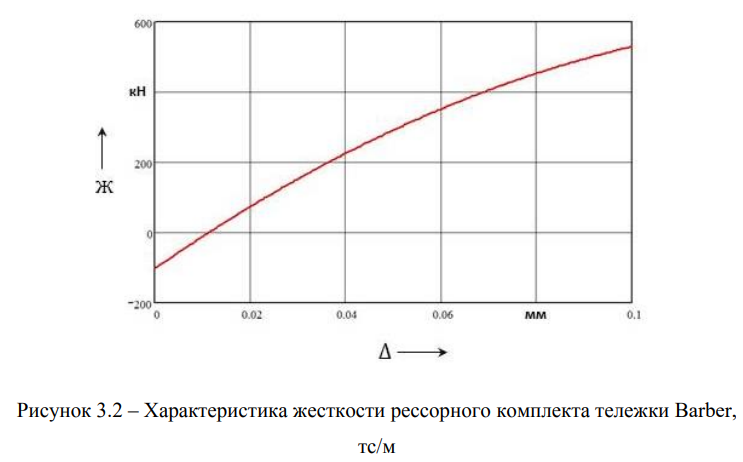
Из представленного выше рисунка вытекает очевидный вывод: рессорное подвешивание кузова вагона на тележках Barber относится к так называемому жесткому типу. Оценим погрешность выполненной аппроксимации. В результате экспериментов, выполненных с участием автора в вагонном ремонтном депо Московка АО «ВРК-2» и данных работы [94], установлено, что жесткость одного рессорного комплекта в груженом режиме вагона равна 447 тс/м. Здесь можно отметить, что жесткость определяется как отношение приращения функции (силы упругости) к приращению деформации рессорного комплекта, причем эти величины берутся немалыми. Так как колебания кузова в груженом режиме его движения происходят около положения статического равновесия, то с учетом амплитуды динамического прогиба рессорного комплекта получаем, что она приблизительно равна ж = 472,7 тс/м. Следовательно, погрешность аппроксимации не превышает 6 %, что вполне допустимо.
Оценка влияния базы тележки на динамику вагона
Расчетная схема системы «вагон-путь» приведена ранее (см. рисунок 2.10). Для рассматриваемого случая дополнительно добавим следующие допущения. Во-первых, ограничимся плоским случаем и, во-вторых, учтем только колебания подпрыгивания кузова. Необходимо отметить, что в учебнике [66] рассматривается линейный вариант подвешивания, допускающий разделение колебаний подпрыгивания и галопирования кузова полувагона при условии геометрической симметрии кузова и при условии, что центр жесткости совпадает с центром тяжести. При нелинейном подвешивании кузова такое разделение в принципе невозможно.
Запишем дифференциальное уравнение для подпрыгивания кузова вагона:

Укажем вероятные явления, которые мы теряем, когда выполняем линеаризацию характеристики силы сухого трения. Из теории систем с сухим трением известно, что оно способно создавать зоны застоя, и поэтому аналитическое исследование движения таких систем чрезвычайно затруднено. Следовательно, мы предполагаем, что энергии, доставляемой в систему внешним воздействием, достаточно для движения кузова вагона без остановок, т.е. вагон всегда совершает колебательные движения.
Силовая характеристика рессорного подвешивания тележки Barber нелинейная, поэтому будем использовать метод гармонического баланса, который требует выполнения энергетического соотношения только на частоте возмущения, которое считаем гармоническим согласно Руководящему документу ВНИИЖТ [73], амплитуда которого может быть выражена в зависимости от длины неровности пути соотношением h = 0,0004 lH, м.
Выполним некоторые несложные преобразования, связанные с внешним возмущением, действующим на колесные пары вагона, что упростит наши дальнейшие выкладки:


Ниже на рисунке 3.3 приведен график изменения амплитуды внешнего возмущения, действующего на вагон.
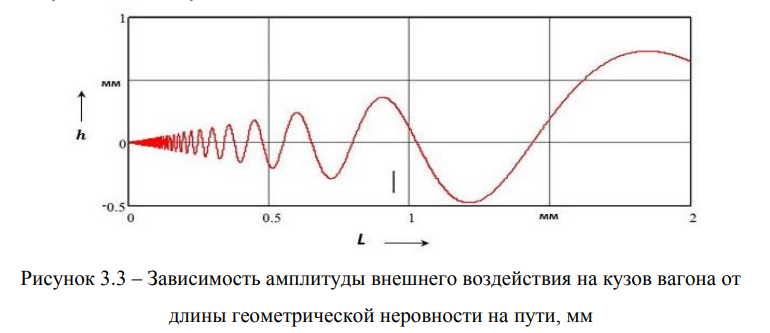
Из приведенного рисунка 3.3 очевидно, что отношение базы тележки к длине геометрической неровности играет важную роль в динамике подвижного состава (рисунок 3.4). Однако выбрать вполне конкретное соотношение невозможно, поскольку на реальном пути — разные длины неровностей, причем амплитуда и длина некоторых из них изменяются непредсказуемым образом.
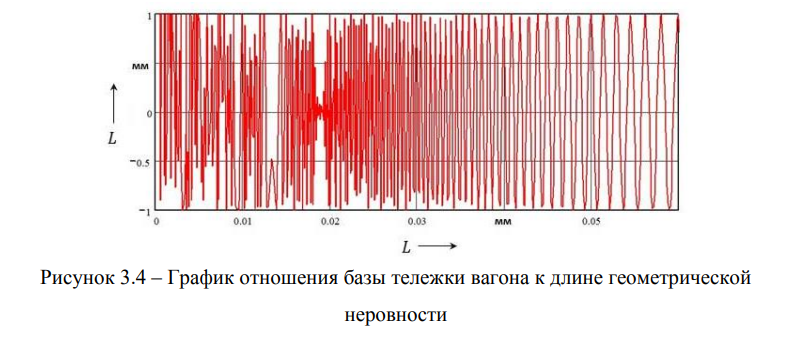
Несмотря на отмеченное, с точки зрения минимизации воздействия неровностей пути на динамику вагона все же можно указать два рациональных значения для отношения базы тележки к длине геометрической неровности. Исходя из того факта, косинус этого отношения, умноженный на 2л, должен быть близок к нулю, имеем, что ¡н= 41 т или ¡н = 41т/3 (в нашем случае такими благоприятными являются величины 7,4 и 2,5 метра). Неблагоприятными будут следующие соотношения — ¡н = 21т или ¡т = ¡н, следовательно, 3,7 и 1,85 метра, что далее легко обнаружить в расчетах, результаты которых приведены на рисунке 3.5.
Здесь необходимо отметить, что указанные соотношения являются приближенными.
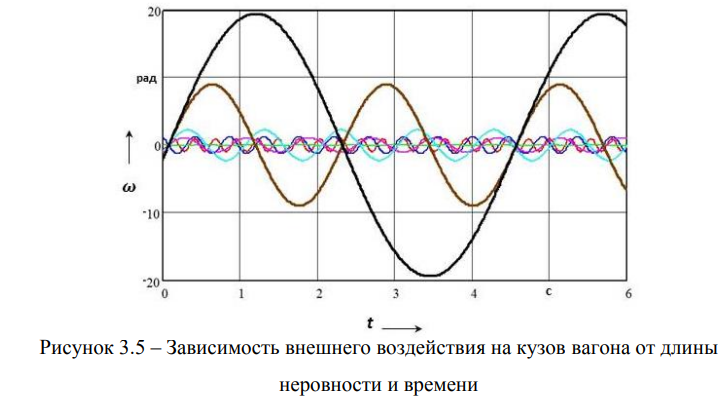
Из анализа рисунка 3.5 видно, что при базе тележки, т.е. при расстоянии между центрами осей колесных пар 1,85 метра, благоприятной длиной геометрической является 7 м. Тогда внешнее возбуждение будет минимальным. Но это утверждение справедливо только в том случае, когда других длин неровностей на железнодорожном пути нет.
Алгоритм формирования методики исследования динамического поведения вагона как системы с нелинейным рессорным подвешиванием
Если обратиться к уравнению (3.3) и учесть принятую аппроксимацию
силовой характеристики рессорного подвешивания тележки Barber в виде
кубического полинома, то нетрудно заметить проблему, связанную с возведением
в степень разности z –. От нее можно избавиться, введя новую переменную
= z – , т.е. прогиб рессорного подвешивания, тогда дифференциальное
уравнение для сжатия рессорного комплекта тележки Barber будет иметь
следующий вид:
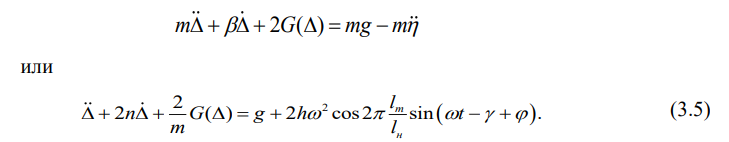

Уравнение (3.6) — приближенное, стационарное решение, так как на самом деле любая периодическая функция, удовлетворяющая условиям Липшица, всегда может быть представлена бесконечным рядом Фурье. Однако следует помнить о том, что здесь строится алгоритм экспертной оценки динамического поведения вагона, следовательно, вполне допустимы некоторые небольшие погрешности.
Необходимо отметить, что в данном случае взят лишь первый гармонический член этого ряда, поэтому и говорится о приближенном решении (3.6) и удовлетворении нелинейного уравнения (3.5) лишь по гармонике возмущения с. В этом, собственно говоря, заключается суть метода гармонического баланса, которым далее следует воспользоваться.
Вспомним некоторые тригонометрические соотношения, которые понадобятся нам в дальнейших преобразованиях:

В силу того, что решение (3.6) должно выполняться в любой момент времени, запишем систему трансцендентных уравнений:

Затем подставим этот результат в выражение собственной частоты колебаний подпрыгивания кузова вагона в консервативном случае, в результате получим собственную частоту подпрыгивания кузова вагона как функцию переменной D0:
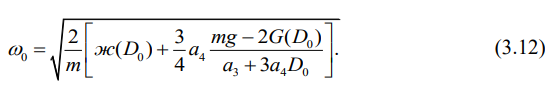
Далее, возводя второе и третье уравнения в квадрат, и складывая
результаты, и учитывая выражение (3.12), найдем целевую функцию для поиска
неизвестных величин (ее вид хорошо знаком специалистам по теории колебаний, что
указывает на корректность проведенных выше выкладок):

Здесь отметим, что по физическому смыслу собственная частота нелинейной системы обязана быть действительной величиной, т.е. должно выполняться следующее неравенство:
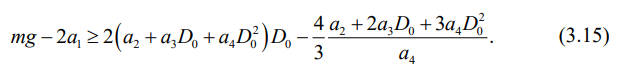
С другой стороны, амплитуда подпрыгивания кузова полувагона А должна быть также действительной величиной, которая должна быть больше или равна нулю, следовательно, имеем еще одно неравенство:
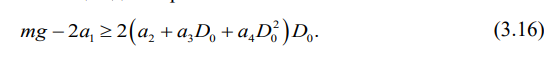
Для запуска итерационного процесса получения корня необходимо знать начальное приближение к корню 00, которое должно выбираться из условия обеспечения сходимости итераций, следовательно, должны выполняться оба неравенства (3.15) и (3.16). Хотя проще это сделать, если решить неравенство (3.15), которое превращается в равенство при отыскании критического значения, ибо это кубическое уравнение, которое, как известно из высшей математики, обязательно будет иметь один действительный и два комплексно-сопряженных корня или три действительных корня.
Поиск значения переменной О0 будем осуществлять, минимизируя целевую функцию (3.14), для этого в пакете MathCAD есть стандартная процедура гоо^…). В результате использования указанной функции имеем график зависимости 00 от скорости движения вагона (рисунок 3.6).
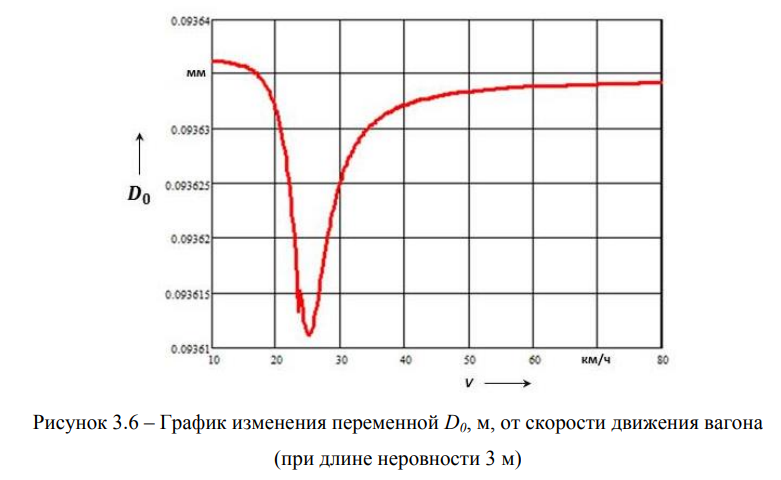
Заметим, что ее изменение не очень велико и близко к статическому прогибу рессорного подвешивания кузова вагона. На рисунке 3.7 показано изменение деформации рессорного комплекта кузова вагона на тележках Barber от его скорости движения. Из него нетрудно видеть, что максимальная амплитуда деформации рессорного комплекта вагона не превышает 4 мм, что вполне совпадает с практикой.
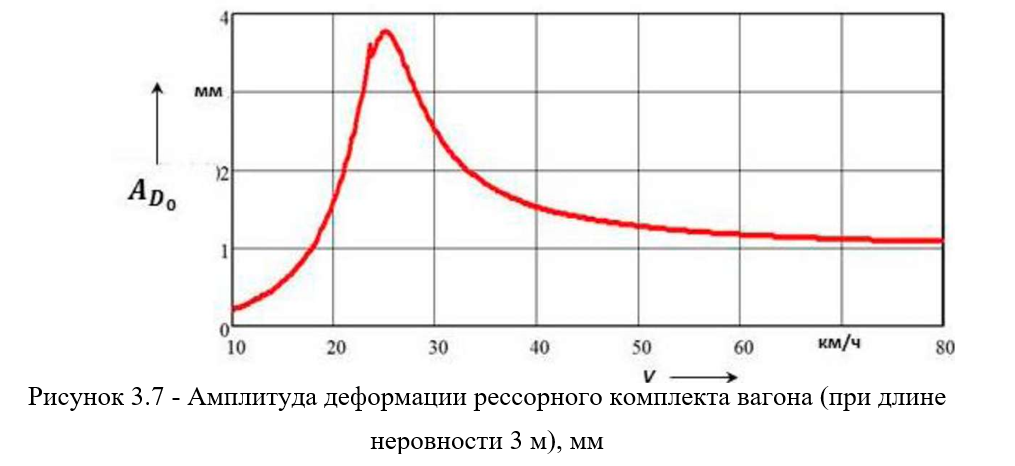
График изменения величины G(D0), создаваемой рессорным подвешиванием вагона, показан на рисунке 3.8.
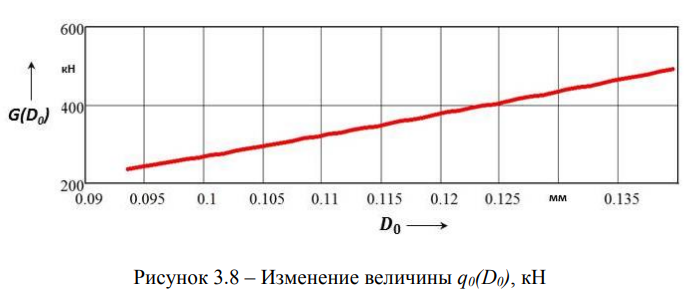

Результаты исследования динамических качеств грузового вагона с нелинейным рессорным подвешиванием
Оценивать динамические качества подвижного состава будем по следующим показателям его динамических качеств: ускорение подпрыгивания кузова вагона, усилие в рессорном подвешивании и давление колесной пары на железнодорожный путь [12].



По полученным формулам выполним расчеты, применяя математический пакет MathCAD. Начнем с того, что аналитически определим статический прогиб рессорного подвешивания вагона, а для этого необходимо вычислить корни кубического уравнения:

Минимальное положительное значение корня и есть статический прогиб рессорного подвешивания кузова вагона, в нашем случае при его массе в 4,6 тс-с2/м (исходим из того факта, что статическая нагрузка от колесной пары на путь составляет 25 тс) имеем fm=91,645 мм. Конечно же, эту операцию проще провести графически, используя силовую характеристику рессорного подвешивания кузова вагона, но результат, разумеется, будет менее точным [66].
Теперь коснемся резонансных скоростей вагона на тележках Barber, учитывая, что он представляется нелинейными дифференциальными уравнениями. Как хорошо известно, в линейном варианте рессорного подвешивания резонанс характеризуется совпадением частот собственной и вынуждающей. В нашем случае рессорное подвешивание описывается нелинейной функцией с четной несимметрией, следовательно, в решении дифференциальных уравнений обязательно будет присутствовать постоянная составляющая, относительно которой и будут происходить колебания подпрыгивания кузова вагона, кроме того, в системе будут возбуждаться гармоники, отличные от собственной частоты линейной консервативной системы. Возникает естественный вопрос: что такое резонанс в нелинейной системе? Корректный ответ на поставленный вопрос такой: это совпадение работ сил трения системы и вынуждающей силы на перемещениях системы. Оставаясь в парадигме линейного подхода, но помня о том, что собственная частота консервативной нелинейной системы зависит от амплитуды подпрыгивания кузова вагона, определим резонансную скорость так:

Очевидно, что резонансная скорость вагона определяется длиной волны геометрической неровности пути и собственной частотой консервативной нелинейной системы, зависящей от амплитуды подпрыгивания кузова. На рисунке 3.9 представлен график собственной частоты подпрыгивания кузова вагона. Вычисления проводились для следующих величин длин волны неровности пути: 1, 3, 5, 7, 12 и 25 м.
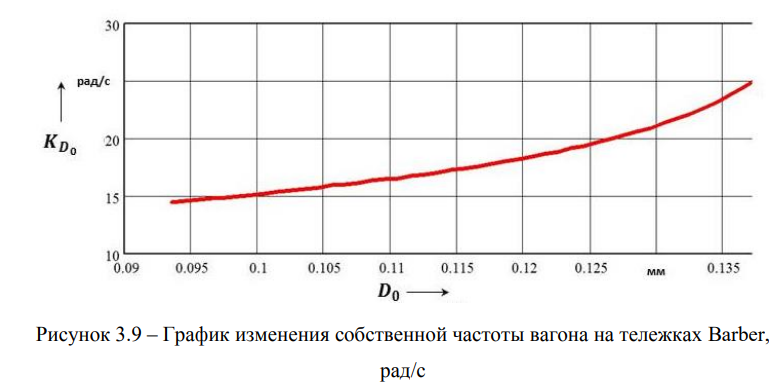
Из графика, приведенного на рисунке 3.9, следует, что собственная частота существенным образом зависит от амплитуды подпрыгивания кузова вагона. Результаты вычислений по формуле (3.27) представлены на рисунке 3.10 (а) и (б).
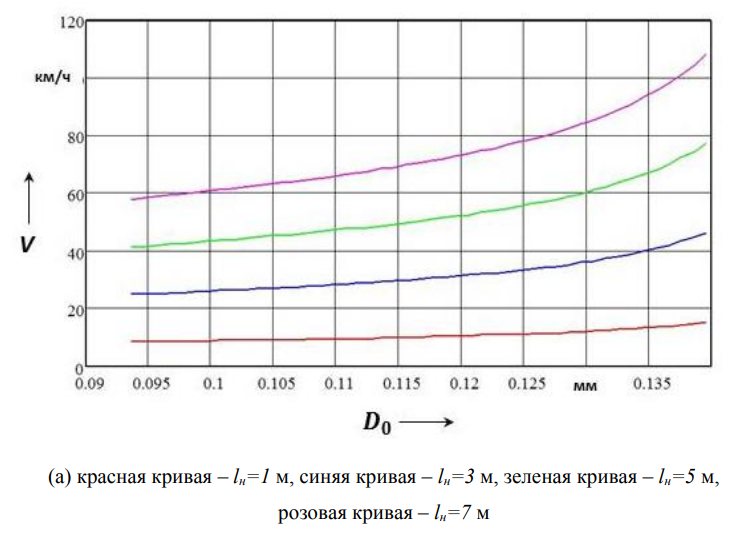
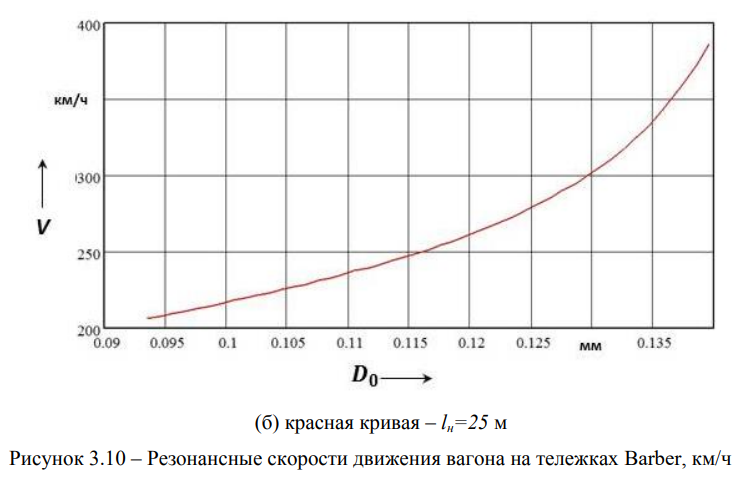
Еще раз отметим, что резонанс может развиваться на суб- и супергармониках, хотя и не так остро, но забывать об этом не следует, особенно когда интерпретируются эмпирические материалы.
Учитывая, что на железнодорожном пути могут встречаться практически любые длины геометрических неровностей, то с большой долей вероятности можно утверждать, что любой вагон с нелинейным рессорным подвешиванием всегда движется в составе поезда в резонансном режиме, величины амплитуд которых ограничиваются диссипативными силами и нелинейностью в подвешивании. Это первый вывод наших исследований. Ниже (рисунок 3.11) приводятся результаты исследований вертикальной динамики вагона на тележках Barber для конкретной длины неровности, равной трем метрам, как наиболее часто встречающейся на железнодорожном пути, а амплитуда неровности принималась согласно регрессионному уравнению h = 0,00041н, и равна h = 1,2 мм. Такая длина неровности также может определяться часто встречающимся в практике неравномерным прокатом поверхности катания колес.
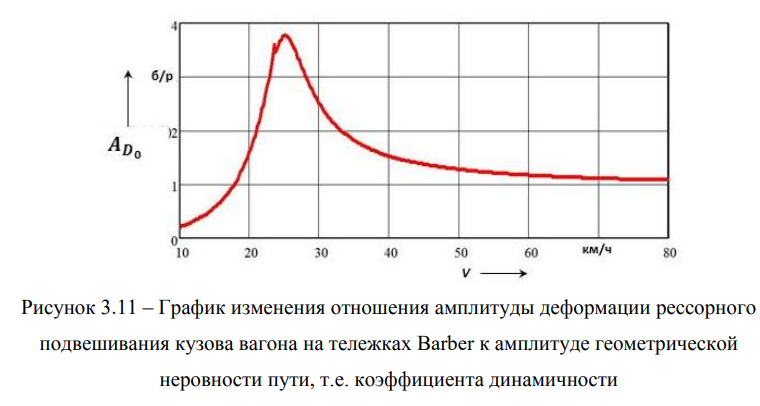
Очевидно, что в системе может развиваться резонанс при скорости движения вагона 27 км/ч, что подтверждается на рисунке 3.10 (а) (см. синюю кривую).
На рисунке 3.12 дается график деформации рессорного подвешивания кузова вагона на тележках Barber, причем красная кривая соответствует указанным выше условиям резонанса (V = 27 км/ч).
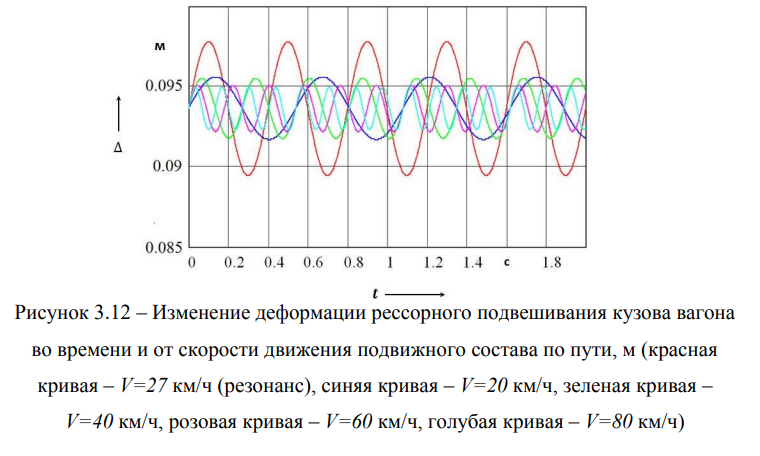
Сдвиг фазы между вынужденными колебаниями и возбуждающей силой представлен на рисунке 3.13.
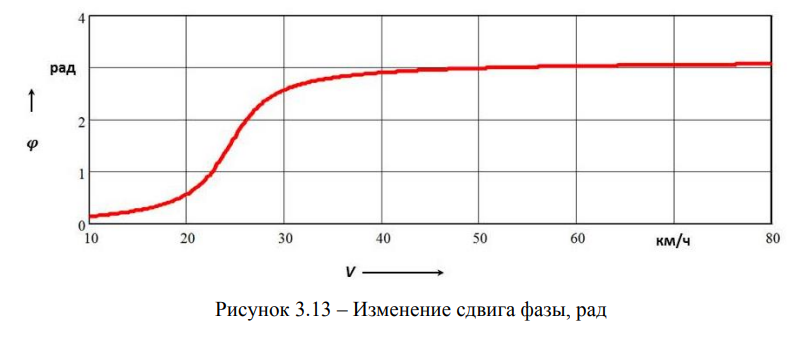
Этот график убеждает нас в том, что приведенные выше вычисления выполнены корректно, так как он имеет привычный для специалистов по теории колебаний вид.
На рисунке 3.14 показан график коэффициента динамичности системы по силе (он также имеет привычный для специалистов по теории колебаний вид).
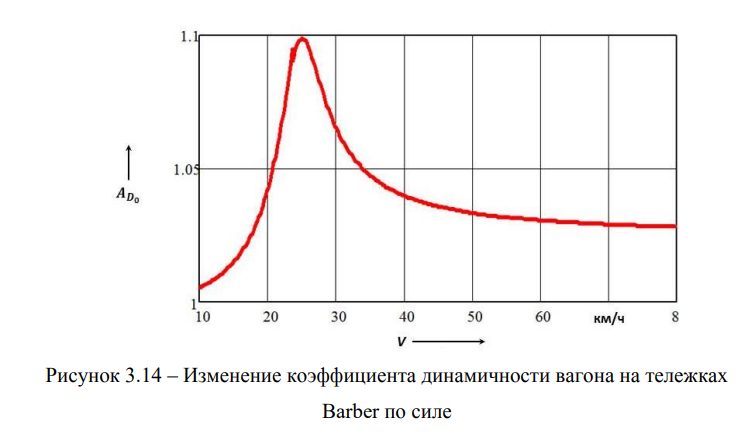
Если бы на пути не встречались другие длины геометрических неровностей, то такой график коэффициента динамичности по силе можно было бы считать идеальным, так как усилие, развиваемое рессорным подвешиванием вагона, очень мало отличается от статического, меньше которого быть в реальности не может.
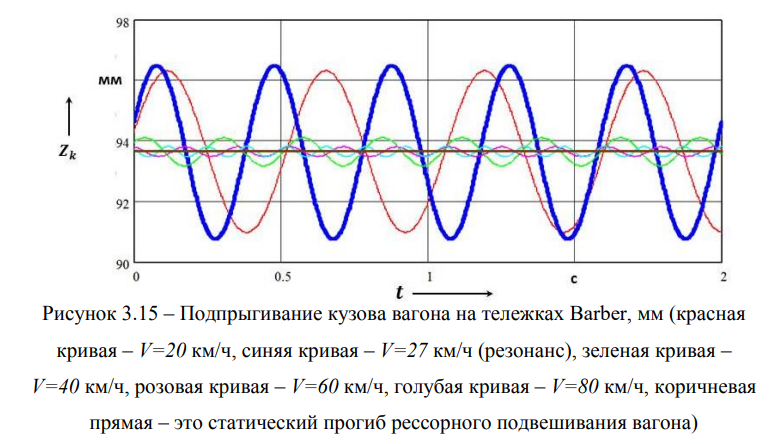
Заметим, что колебания подпрыгивания кузова вагона на тележках Barber происходят относительно положения, которое мало отличается от статического (см. рисунок 3.15). Далее приведем график ускорения подпрыгивания кузова вагона на тележках Barber в долях g (рисунок 3.16).
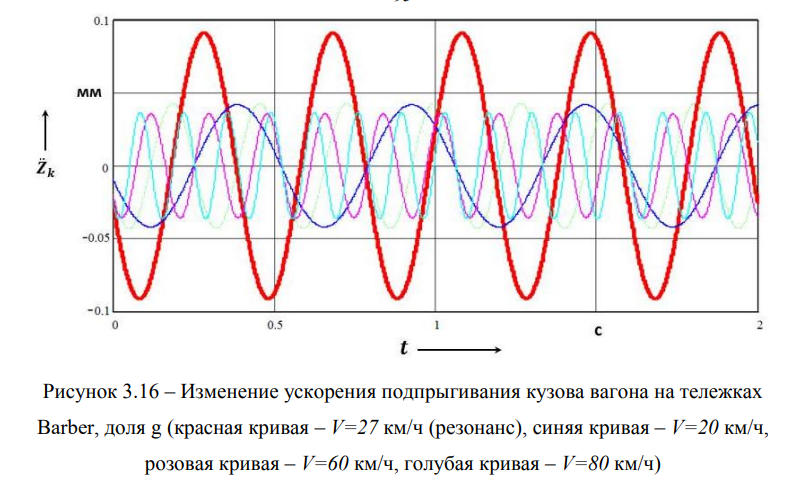
Уровень ускорения кузова вагона при движении по геометрической неровности длиной 3 м можно охарактеризовать диапазоном от 0,014g до 0,104g в заданном диапазоне скоростей движения грузовых поездов от 10 км/ч до 80 км/ч. Следовательно, с ростом скорости движения вагона в указанном диапазоне скоростей уровень ускорения кузова вагона на тележках Barber возрастает практически в 10 раз. Коэффициент динамичности по ускорению кузова вагона на тележках Barber при движении по совокупности геометрических неровностей с длинами от 1 м до 25 м приведен ниже (рисунок 3.17).
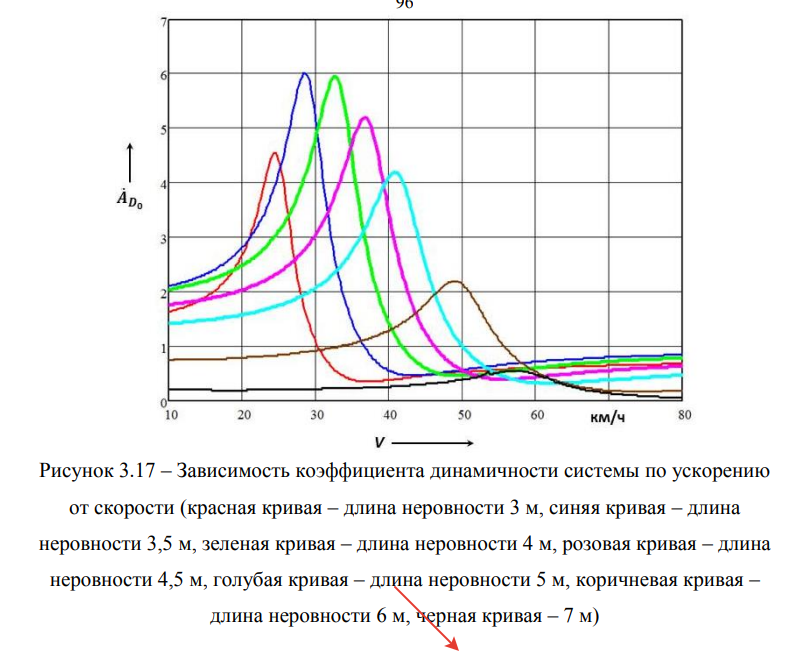
Очевидно, что мы не можем выделить какую-либо одну конкретную кривую, так как трудно определить, какие длины геометрических неровностей присутствуют на конкретном участке железной дороги (путеизмеритель, во- первых, фиксирует суммарные неровности (совокупность геометрических и силовых), и, во-вторых, нагрузка на ось вагона-путеизмерителя составляет 18 тс в отличие от соответствующей нагрузки груженого вагона, что не отражает реального состояния пути под действующими осевыми нагрузками 23,5 и 25 тс). Однако можно с уверенностью утверждать, что коэффициент динамичности по ускорению в рассматриваемом диапазоне скоростей движения вагона изменяется в пределах от 6 до 1. Ниже на рисунке 3.18 представлено отношение амплитуды ускорения кузова вагона на тележках Barber к ускорению свободно падающего тела, т.е. g.
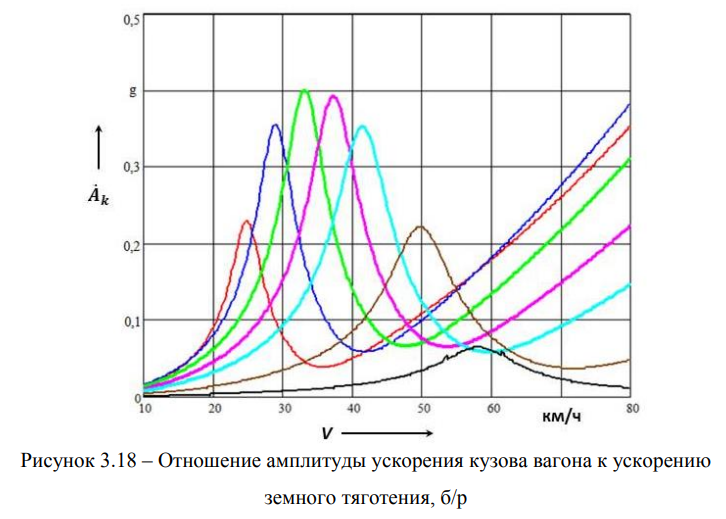
Нетрудно заметить, что в диапазоне скоростей движения вагона от 10 до 80 км/ч ускорение кузова сначала возрастает, причем максимум обнаруживается при длине геометрической неровности 4 м, затем оно несколько падает, в дальнейшем вновь возрастает, но не известно, до каких величин, так как скорости движения подвижного состава свыше 80 км/ч не являются эксплуатационными.
Далее представлен коэффициент динамичности вагона на тележках Barber по перемещению (рисунок 3.19).
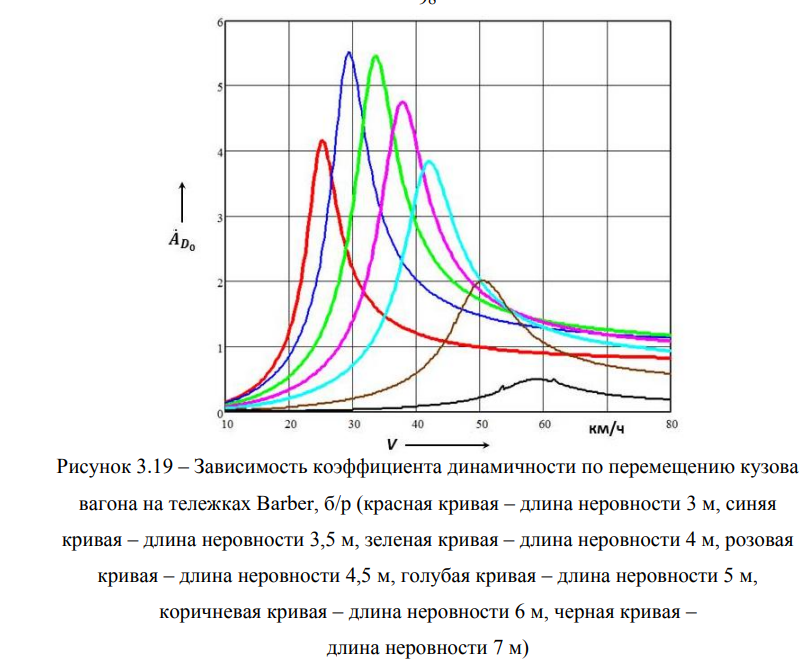
Информация, представленная на рисунке 3.19, позволяет сделать вывод о том, что коэффициент динамичности системы по перемещению изменяется в пределах от 5,51 до 1,17 в диапазоне скоростей от 10 км/ч до 80 км/ч.
На рисунке 3.20 дана зависимость коэффициента динамичности вагона на тележках Barber по силе в рессорном подвешивании.
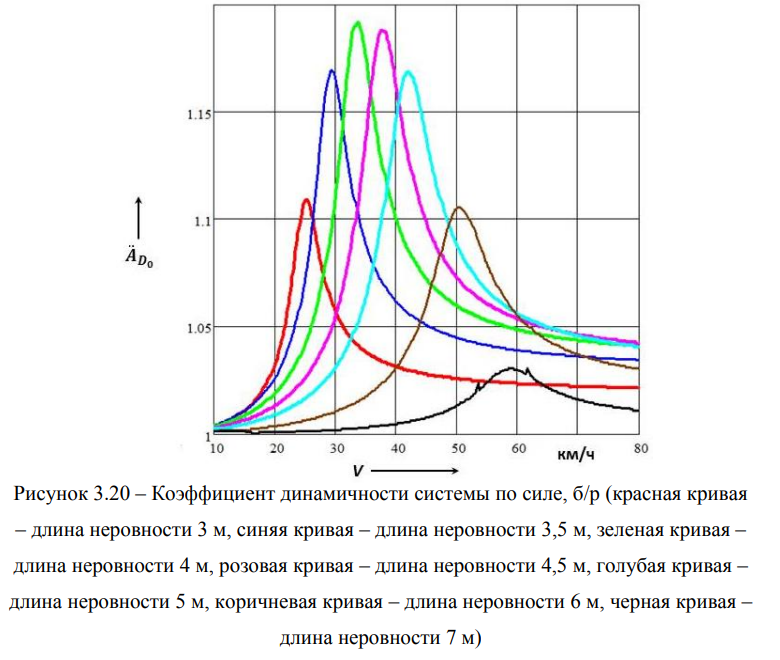
Область значений данного коэффициента динамичности находится в пределах от 1,19 до 1,04 при изменении скорости движения вагона с 10 км/ч до 80 км/ч.
Последней характеристикой экспертной оценки является воздействие на железнодорожный путь вагона на тележках Barber. Эта характеристики в виде двух составляющих представлены ниже на рисунках 3.21 и 3.22.
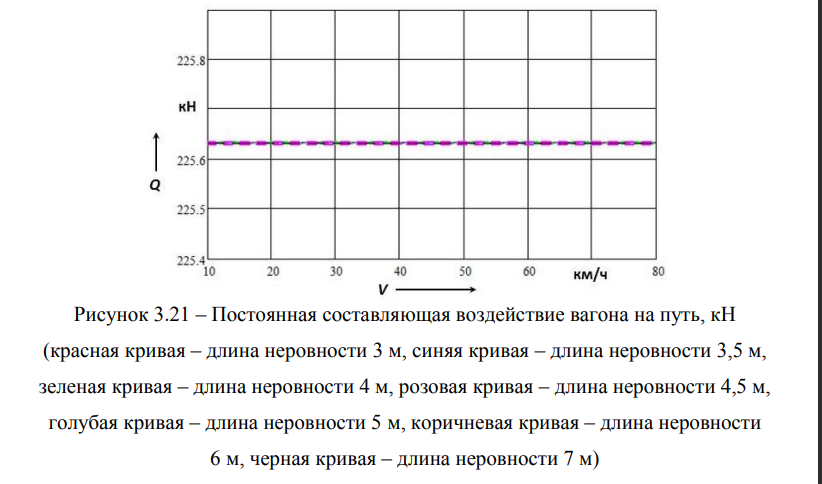
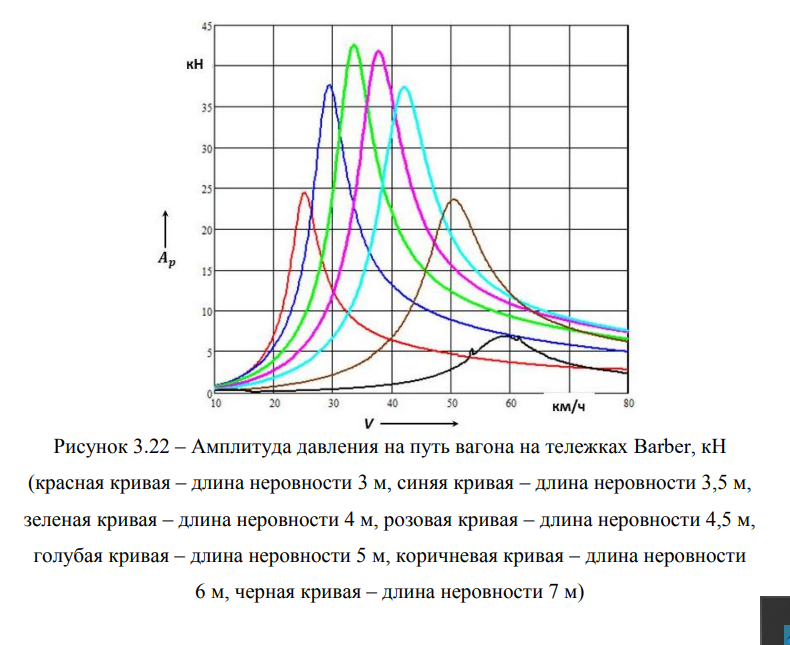
Постоянная составляющая давления вагона на железнодорожный путь не зависит ни от скорости движения, ни от длины геометрической неровности на рельсах. Амплитуда давления колесной пары вагона на путь при ее безотрывном движении по рельсам с ростом скорости движения сначала возрастает, а затем начиная со скорости 70 км/ч падает. Наибольшее значение равно 42,529 кН (4,34 тс). Резонанс, если о нем вообще можно говорить в нашем нелинейном случае, обнаруживается при скорости 35 км/ч, что соответствует длине неровности 4 м. Максимальное давление на путь составляет порядка 259 кН (26,4 тс).
Динамические свойства вагона при учете неравножёсткости пути по
его длине
В применяемых в настоящее время для исследования динамики подвижного состава расчётных схемах полагается, что жёсткость пути является величиной постоянной, в крайнем случае, — нелинейной величиной от его прогиба.
Многочисленные экспериментальные исследования, выполненные ранее такими научными организациями как: ВНИИЖТ, ДИИТ, ЛИИЖТ, МИИТ, ОмИИТ и другими, посвящённые измерениям вертикальной жёсткости железнодорожного пути, указывают на то, что она не является постоянной величиной по длине рельсового звена, а представляет собой некоторый случайный процесс, в котором можно обнаружить скрытые периодические компоненты. В работе [11] по экспериментальным осциллограммам насчитали, что колёсная пара совершает около 25 колебаний при длине рельса 12,5 м и около 50 колебаний при длине рельса 25 м. Таким образом, шпальная неравно-упругость железнодорожного пути объясняется его физическим устройством. Другие составляющие в спектре жёсткости пути пока не имеют строгого физического объяснения, поэтому будем в дальнейшем учитывать только шпальную неравноупругость железнодорожного пути.
Итак, в нулевом приближении учтём только неравножёсткость пути из-за наличия шпал (так как она имеет простое физическое и понятное всем объяснение), остальные составляющие неравноупругости пока не будем учитывать поэтому представим жёсткость пути в следующем виде:
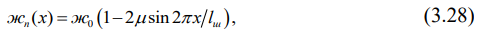
где ж0 — средняя на звене жёсткость пути, при этом, если удастся найти её зависимость от скорости движения подвижного состава, то тогда можно вести речь не о статической, а о динамической его жёсткости; / — коэффициент параметрического возбуждения (как показывает опыт — это всё же малая величина), 1ш — расстояние между серединами шпал (обычно определяется эпюрой шпал, в нашем случае 1ш = 0,54 м). Из формулы (3.28) следует, что начало отсчёта взято в середине междушпального ящика.
Давая экспертную оценку воздействию на путь вагона, мы имеем моральное право оценить дополнительную динамическую добавку давления на путь, возникающую из-за переносного ускорения колесной пары, являющегося результатом аддитивного воздействия шпальной неравноупругости пути на экипаж [55]. Другими словами, на рисунке 3.23 дан график изменения дополнительной динамической добавки давления на неравноупругий путь от скорости движения вагона.
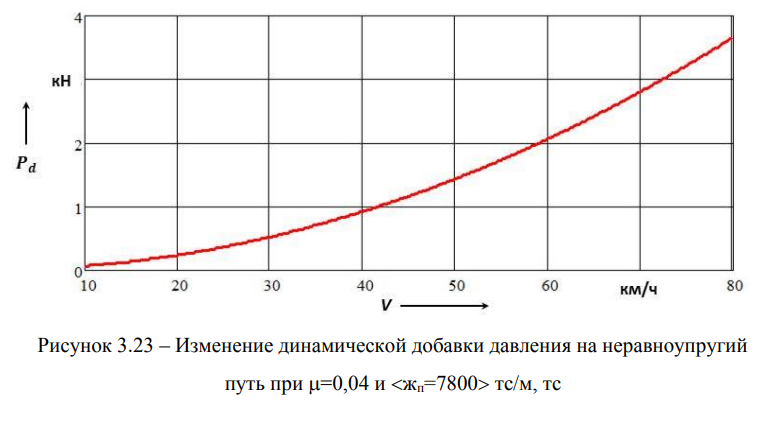
Очевидно, что с ростом скорости данная добавка монотонно возрастает и достигает при скорости движения вагона 80 км/ч величины 3,63 тс. Если сюда прибавить динамическую добавку от геометрических неровностей, которая равна 4,3 тс, то получим, что максимум суммарной динамической добавки может достигать 4,43 тс при 80 км/ч и 4,93 тс при резонансной скорости 33,4 км/ч.
Если принять, что экипаж движется по неравноупругому по протяженности пути (шпальная неравноупругость) с геометрическими неровностями рельсовых нитей, то математическая модель, описывающая колебания подпрыгивания кузова, имеет вид:
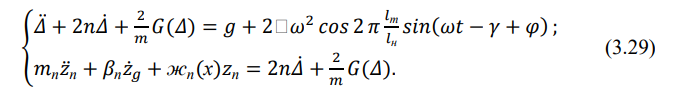
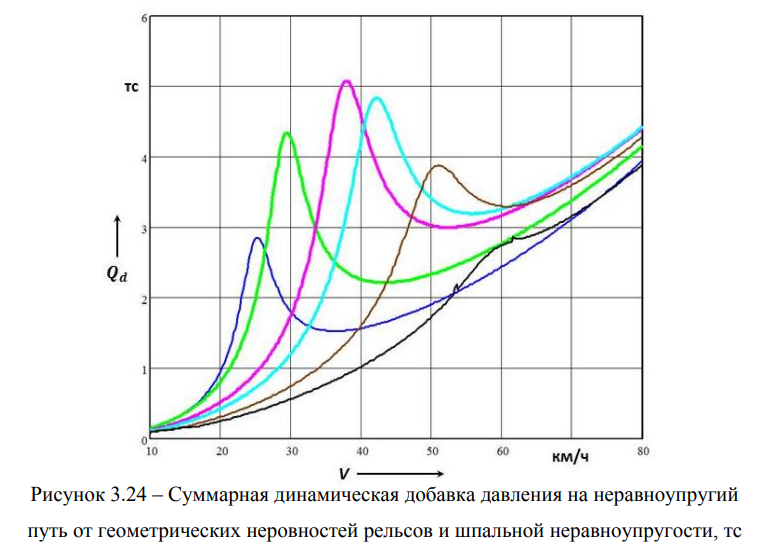
Суммарное действие геометрических неровностей пути и ее шпальной неравноупругости представлено на рисунке 3.24.
Выводы
Таким образом, в результате сформированных математических моделей механической колебательной системы «вагон-путь» выполнен сравнительный мониторинг показателей динамических качеств порожних и груженых вагонов (типового и инновационного) при движении их по пути с неровностями, задаваемых согласно Руководящему документу ВНИИЖТ и по равноупругому пути. Установлено, что инновационные вагоны в порожнем режиме их движения обладают значительно лучшими динамическими свойствами. Если резонансный режим движения типового порожнего вагона приходится на скорость 58 км/ч, то для инновационного вагона с тележкой 18-9855 он приходится на стадию набора скорости поезда 32 км/ч.
Заметим здесь, что учет неравноупругости железнодорожного пути по его длине, если рассматривать полноразмерную пространственную модель колебаний механической колебательной системы «вагон-путь», сразу приводит к тому, что исследование дифференциальных уравнений с переменными, и, в общем случае, — случайными коэффициентами, чрезвычайно существенным образом усложнит их интегрирование. Здесь, чтобы оценить реально динамические качества вагона на тележках «Barber» нужно, кроме нелинейных дифференциальных уравнений движения, иметь реальные реализации геометрических неровностей пути, которые будут разными для различных участков железных дорог.
Итак, разработана методика нахождения экспертных оценок динамических качеств нового подвижного состава, на основании которой создан алгоритм расчетов и написана программа в среде MathCAD.
При этом следует учесть, что железнодорожный путь в действительности не является равноупругим, а внесение данного фактора в математическую модель поведения подвижного состава сразу приводит к тому, что исследование дифференциальных уравнений с переменными, а может быть, случайными коэффициентами чрезвычайно существенным образом усложнит их интегрирование, особенно если рассматривать полноразмерную пространственную модель колебаний механической колебательной системы «вагон-путь». Здесь, чтобы оценить реально динамические качества вагона на тележках Barber, нужно, кроме нелинейных дифференциальных уравнений движения, иметь реальные реализации геометрических неровностей пути, которые будут разными для различных участков железных дорог.
Методом гармонического баланса выполнен анализ показателей динамических качеств инновационного грузового вагона как системы с нелинейным рессорным подвешиванием при движении по неровностям пути. Установлено, что отношение базы тележки к длине геометрической неровности играет важную роль в динамике подвижного состава. Выявлены благоприятные и неблагоприятные значения этих соотношений, в частности:
- получено установившееся решение уравнения нелинейных колебаний вагона, содержащее константу, зависящую от того, что нелинейная силовая характеристика обладает четной несимметрией, а также и от силы тяжести кузова;
- получена нелинейная зависимость собственной частоты колебаний подпрыгивания от постоянной, зависящей от силы тяжести кузова и от амплитуды его подпрыгивания;
- выявлены показатели динамических качеств инновационного вагона как нелинейной колебательной системы, которые отражают значительное его преимущество по сравнению с типовым вагоном. Так, например, его максимальные коэффициенты динамичности по перемещению (подпрыгиванию) кузова и по силе давления на путь приходятся на стадию разгона поезда, в то время как для типового вагона такой режим приходится на диапазон установленной скорости;
- получено значение суммарной динамической добавки давления колесной пары на неравноупругий путь, зависящей от геометрических неровностей рельсов и от вертикальной неравноупругости рельсошпальной решетки.
Полученные результаты исследований динамической нагруженности вагонов с разными типами тележек, в том числе системы «вагон-путь», с нелинейным рессорным подвешиванием ходовой части во многом определяют причинную основу отцепок грузовых вагонов во внеплановый ремонт. Стоит напомнить, что сравнительная оценка показателей эксплуатации вагонов ТВСЗ и вагонов модели 12-132 показывает, что вагоны Тихвинского ВСЗ вследствие обнаруженных неисправностей отцепляются в 5,7 раз реже, чем вагон 12-132, в том числе по колесным парам — реже в 4,1 раза; по неисправностям буксового узла — реже в 6,8 раза; по неисправностям тележки — реже в 53,5 раза; по неисправностям автотормозов — реже в 2,7 раза; по кузову и раме — реже в 8,2 раза.
Список литературы
- Нехаев, В.А. Определение резонансных скоростей подвижного состава / В.А. Нехаев // Известия Транссиба. — 2016. — № 4(28). — С. 10-22.
- Николаев, В.А. Разработка методов аналитического конструирования квазиинвариантных систем рессорного подвешивания железнодорожных экипажей: диссертация … доктора технических наук: 05.22.07 / В.А. Николаев. — Омск, 2003. — 371 с.
- Нормы расчета и проектирования грузовых вагонов железных дорог колеи 1520 мм Российской Федерации. — М.: ВНИИЖТ, ГосНИИВ, 2004. — 212 с.
- Об установлении гарантийных участков: Указание МПС РФ от 1997 № А- 369у.
- Павлюков, А.Э. Прогнозирование нагруженности ходовых частей грузовых вагонов повышенной грузоподъемности методами имитационного моделирования: диссертация … доктора технических наук: 05.22.07 / А.Э. Павлюков. — Екатеринбург, 2002. — 372 с.
- Пахомов, М.П. Результаты экспериментальных исследований упругих характеристик пути на Забайкальской железной дороге / М.П. Пахомов, И.И. Галиев [и др.] // Материалы сетевой научно-технической конференции «Динамика и меры повышения эксплуатационной надежности локомотивов в условиях железных дорого Урала и Сибири». — Омск: Омский ин-т инж. ж.-д. транспорта, 1972. — С. 139-146.
- Петров, Г.И. Оценка безопасности движения вагонов при отклонениях от норм содержания ходовых частей и пути: диссертация … доктора технических наук: 05.22.07 / Г.И. Петров — М.: МИИТ, 2000. — 353 с.
- Повышение эффективности и надежности вагонов в эксплуатации: научно- исследовательская работа [Электронный ресурс] // ЕГИСУ НИОКТР. — Режим доступа: https://esu.citis.ru/nioktr/-0120010658000000000000-.
- Положение о системе технического обслуживания и ремонта грузовых вагонов, допущенных в обращение на железнодорожные пути общего пользования в международном сообщении [Электронный ресурс] // Совет по железнодорожному транспорту государств-участников Содружества. — 2012. — Режим доступа: http://docs.cntd.ru/document/902326053.
- Порядок ведения раздельного учета доходов и расходов и финансовых результатов по видам деятельности, тарифным составляющим и укрупненным видам работ ОАО «РЖД»: Приказ Минтранса России от 31 декабря 2010 г. № 311 [Электронный ресурс] // СПС «КонсультантПлюс». — Режим доступа: http://www.consultant.ru/document/cons doc LAW 73986/.
- Правила технической эксплуатации железных дорог Российской Федерации: утверждены Приказом Минтранса России от 21 декабря 2010 г. N 286 [Электронный ресурс] // СПС «КонсультантПлюс». — Режим доступа: http://www.consultant.ru/document/cons_doc_LAW_110021/3ade8a9c6782a267 62a87fca524237a54e0ef6ed/.
- РД 32 ЦВ 052-99: Инструкция по ремонту тележек грузовых вагонов. — М.: Департамент вагонного хозяйства МПС РФ, 1999. — 87 с.
- РД 32.68-96: Расчетные неровности железнодорожного пути для использования при исследованиях и проектировании пассажирских и грузовых вагонов. — М.: МПС, 1996. — 17 с.
- Савоськин, А.Н. Об учете влияния характеристик пути на возмущения, вызывающие вертикальные колебания рельсовых экипажей / А.Н. Савоськин // Научные труды МИИТа. — 1970.- № 329. — С. 14-33.
- Соколов, А.М. Научные основы создания и оценки эффективности внедрения инновационных вагонов / А.М. Соколов // Бюллетень ОУС ОАО «РЖД». — 2015. — № 2. — С. 1-12.
- Способ измерения путеизмерительным вагоном жесткости рельсового пути: патент на изобретение №2240244 / А.М. Боронахин, В.И. Гупалов, А.В. Казанцев, А.В. Мочалов; дата подачи заявки: 28.11.2002; дата начала действия: 28.11.2002; опубликовано: 20.11.2004.
- Способ инерциальных измерений неровностей рельсового пути: патент на изобретение №2242391 / А.М. Боронахин, В.И. Гупалов, А.В. Мочалов; заявка: 2002135945/11, 30.12.2002 (24); дата начала отсчета срока действия патента: 30.12.2002 (45); опубликовано: 20.12.2004.
- Способ оценки состояния железнодорожного пути: патент на изобретение №2394120 / Ю.С. Ромен, Я.М. Клебанов, В.С. Бородин, А.И. Гасанов; дата подачи заявки: 2008-09-11; опубликовано: 10.07.2010.
- Стратегия развития железнодорожного транспорта в Российской Федерации до 2030 года: утверждена Распоряжением Правительства Российской Федерации от 17 июня 2008 г. N 877-р [Электронный ресурс] // СПС «КонсультантПлюс». — Режим доступа: http: //www.consultant.ru/docu- ment/cons doc LAW 92060/4fa0a1723fc315e72f8bd97e119a1101f59ac132/.
- Суслов, Г.К. Основы аналитической механики / Г.К. Суслов. — М.: Гостехиздат, 1944. — 655 с.
- Терешина, Н.П. Расходы инфраструктуры железнодорожного транспорта: Учебное пособие для студентов вузов железнодорожного транспорта / Н.П. Терешина. — М.: УМЦ ЖДТ, 2010. — 224 с.
- Тимошенко, С.П. Колебания в инженерном деле / С.П. Тимошенко, Д.Х. Янг, У. Уивер; под ред. Э.И. Григолюка. — М.: Машиностроение, 1985. — С. 83, 472.
- Устьянцев, С.В. Эра Лоренцо / С.В. Устьянцев, Н.В. Першхайло. — Н.Тагил.: АО «НПК «Уралвагонзавод» им. Дзержинского Ф.Э., 2012. — 193 с.
- Ушкалов, В.Ф. Расчетные возмущения для оценки динамических качеств грузовых вагонов / В.Ф. Ушкалов, Л.Г. Лапина, И.А. Мащенко // Наука и прогресс транспорта. Вестник Днепропетровского национального университета железнодорожного транспорта. — 2013. — № 4 (46). — С. 135¬144.
- Ушкалов, В.Ф. Статистическая динамика рельсового экипажа / В.Ф. Ушкалов, Л.М. Резников, С.Ф. Редько. — Киев: Наукова думка, 1982. — 360 с.
