Цикл статей:
Глава 1 — Вибродиагностика балочных пролетных строений
железнодорожных мостов
Глава 2 — Технические средства измерений и обработки колебаний конструкций мостов
Глава 3 — Натурные эксперементальные исследования динамических воздействий на балочные пролетные строения железнодорожных мостов
Глава 4 — Расчет балочных пролетных строений
Глава 5 — Методики вибродиагностики балочных пролетных строений железнодорожных мостов
Расчет железнодорожных железобетонных путепроводов
Далее приводятся результаты расчетного анализа несущих конструкций двух путепроводов через автодорогу на 56-м и 96-м километре однопутной железнодорожной линии Кульсары-Тенгиз [126, 127].
В результате проделанной работы получены НДС в элементах железобетонных конструкций и АЧХ балочных пролетных строений при заданных нагрузках с использованием пространственных конечно- элементных моделей.
Расчетные модели для анализа НДС и модального анализа сооружения построены согласно данным, предоставленным в виде рабочей документации для рассматриваемого сооружения. Общий вид расчетной модели рассматриваемого сооружения, составленной в лицензионной программе ABAQUS/Standard, представлен на рисунке 4.1 [47].
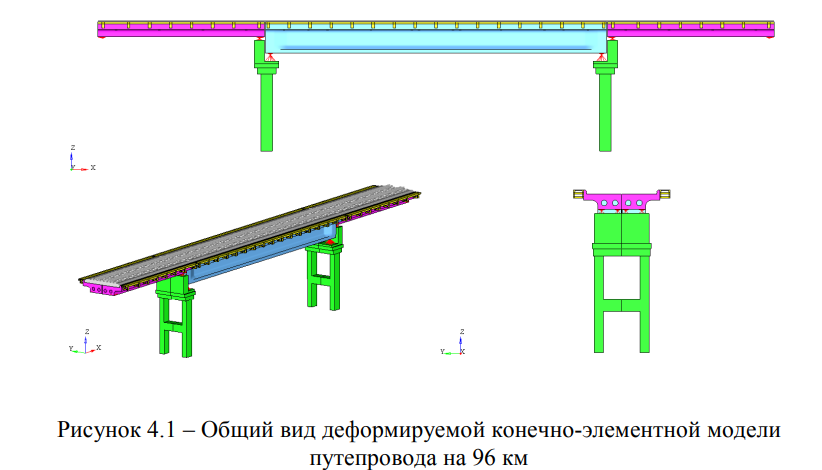
Программный комплекс ABAQUS/Standard в настоящее время апробирован и используется в проектных и научно-исследовательских организациях при расчетах НДС различных сооружений, в том числе и мостов.
Автор выражает признательность Камышову Юрию Александровичу за ценные консультации при разработке конечно-элементных моделей транспортных сооружений и выполнении проверочных расчетов.
Модели железобетонных элементов несущих конструкций путепровода на 96 км однопутной железнодорожной линии Кульсары-Тенгиз, учитывают совместную работу армирующих элементов и бетонного заполнения (Рисунок 4.3).
Бетонное заполнение конструкций железобетонных балочных пролетных строений 11,50 м и 23,60 м путепровода, заданы объемными элементами.
Армирующие элементы конструкций (каркасы, сетки, пучки проволок для предварительного напряжения бетона) пролетных строений заданы стержневыми элементами и учитывают их пространственное расположение в бетонном заполнении.
А) Пролетное строение длиной 23,60 м (на 56-м и 96-м км) Модель блока пролетного строения 23,60 м представлена на рисунках 4.2 и 4.3. Конечно-элементная сетка бетона блока учитывает наличие отверстий для водоотводных трубок (Рисунок 4.3).

Армирующие элементы выделены в группы (Рисунок 4.4) согласно назначенным классам: — напрягаемая арматура (пучки из 24 проволок 05 В11 с установкой в массив бетона при помощи каркасно-стержневых анкеров) и арматура классов А1, А11.

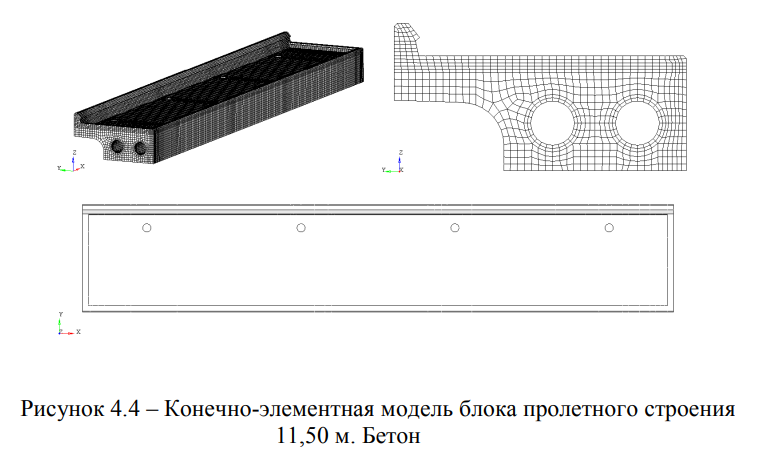
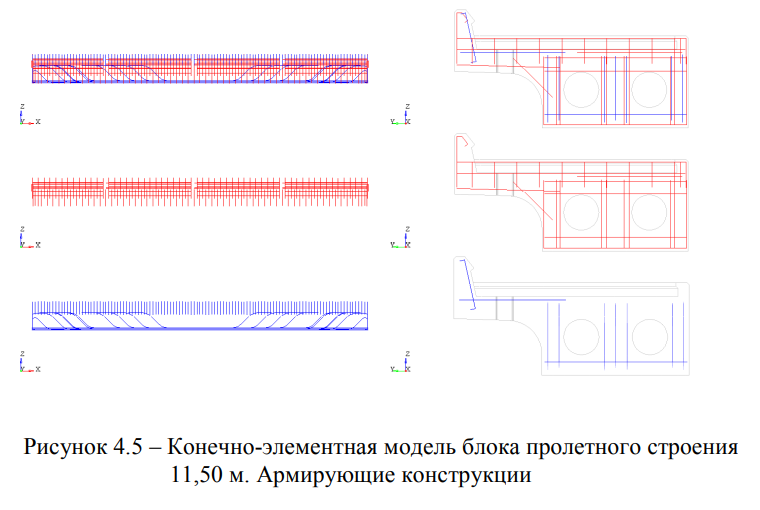
Б) Пролетное строение длиной 11,50 м (на 96-м км) Модель блока пролетного строения 11,50 м представлена на рисунках 4.4 и 4.5. Модель блока пролетного строения 11,50 м представлена на рисунках 4.4 и 4.5. Конечно-элементная сетка бетона блока учитывает наличие отверстий для водоотводных трубок (Рисунок 4.4). Армирующие элементы выделены в группы (Рисунок 4.5) согласно назначенным классам А1, А11.
В) Пролетное строение длиной 16,50 м (на 56-м км)
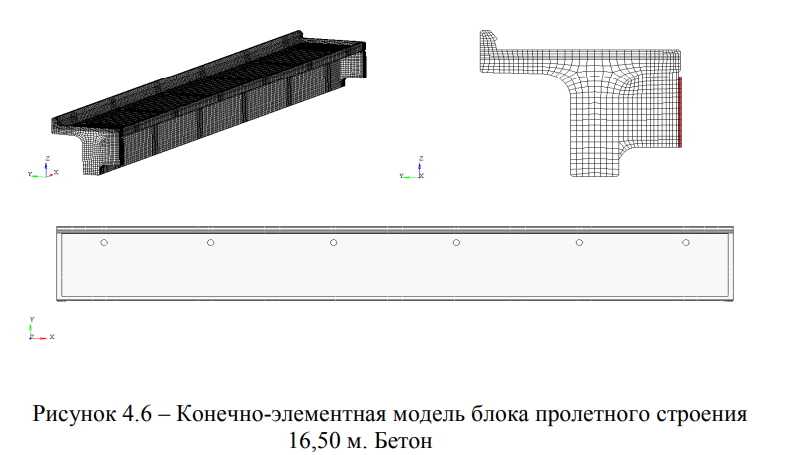
Модель блока пролетного строения 16,50 м представлена на рисунках 4.6 и 4.7. Конечно-элементная сетка бетона блока учитывает наличие отверстий для водоотводных трубок (Рисунок 4.6). Армирующие элементы выделены в группы (Рисунок 4.7) согласно назначенным классам А1, А11.

Конструкционные материалы
Принятые в расчетах физико-механические свойства материалов элементов конструкций путепровода представлены в таблице 4.1.

Нагрузки на обращаемом участке
Все значения нагрузок приняты без учета различных коэффициентов СНиП [121] и СП [122] (условий работы, надежности по нагрузкам, надежности по ответственности и др.).
Временные нагрузки заданы согласно следующим видам воздействий:
- статическая нагрузка от веса сцепа по схеме «локомотив-вагон»;
- статическая нагрузка от веса сплотки из трех локомотивов.
Воздействие от веса локомотива (тепловоза ТЭМ-18, 2 тележки, по 3 оси на тележку) задано в виде сосредоточенных сил 202,7 кН/ось в узлы модели рельсового пути в соответствии с расстояниями: 16900 мм между осями автосцепок; 8800 мм между шкворнями тележек; 1850 мм между осями тележки.

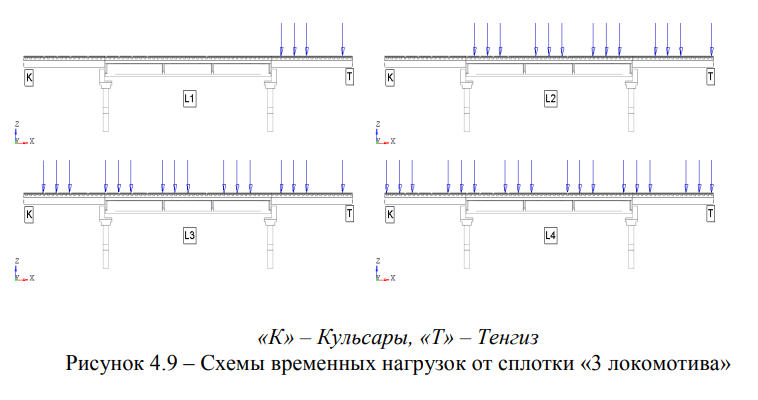
Анализ расчета двух путепроводов А) Статический анализ
Выполнены расчеты напряженно-деформированного состояния элементов сооружения при заданных сочетаниях нагрузок (расчетных случаях). Рассмотрены следующие расчетные случаи (всего 12 случаев; движение сцепа/сплотки от ст. Тенгиз к ст. Кульсары):

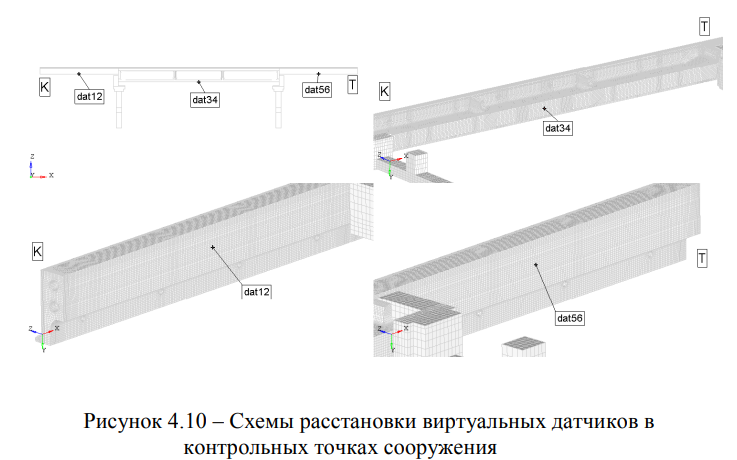
Результаты расчетов представлены в виде значений перемещений и деформаций в контрольных точках, полученных при помощи виртуальных датчиков (податливых стержневых элементов начальной длиной 60 мм с линейно-упругими свойствами стали), установленных на бетоне балочных пролетных строений путепроводов. Контрольные точки выбраны на нижнем поясе в серединных сечениях пролетных строений сооружения (Рисунок 4.10): «dat12» — датчик в середине пролетного строения ПС0-1; «dat34» — датчик в середине пролетного строения ПС1-2; «dat56» — датчик в середине пролетного строения ПС2-3.
Результаты расчетов элементов сооружения при заданных нагрузках представлены в виде распределений напряжений в арматуре и бетоне блоков пролетных строений путепровода на 96-м км для расчетного случая П0 (Приложение Б) и в виде значений перемещений, деформаций и напряжений в контрольных точках и виртуальных датчиках для всех рассмотренных расчетных случаев (Таблицы Б-1 и Б-2 в Приложении Б) [19].
Б) Модальный анализ
Выполнены расчеты форм и частот собственных колебаний сооружения при предварительном нагружении постоянными нагрузками (П0: «Натяжение арматуры блоков 23,60 м + Собственный вес») [58, 75, 128].
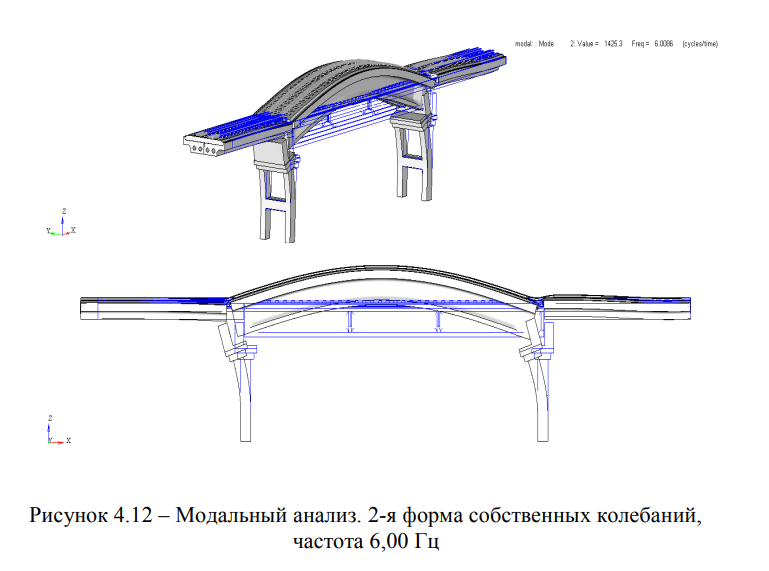
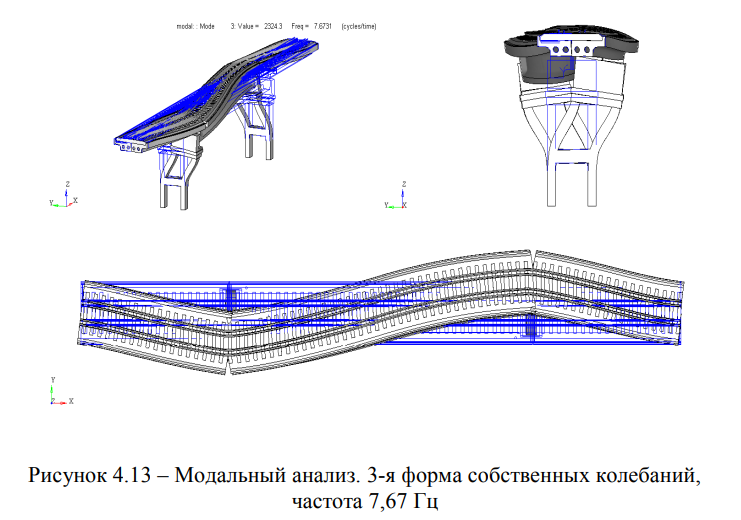
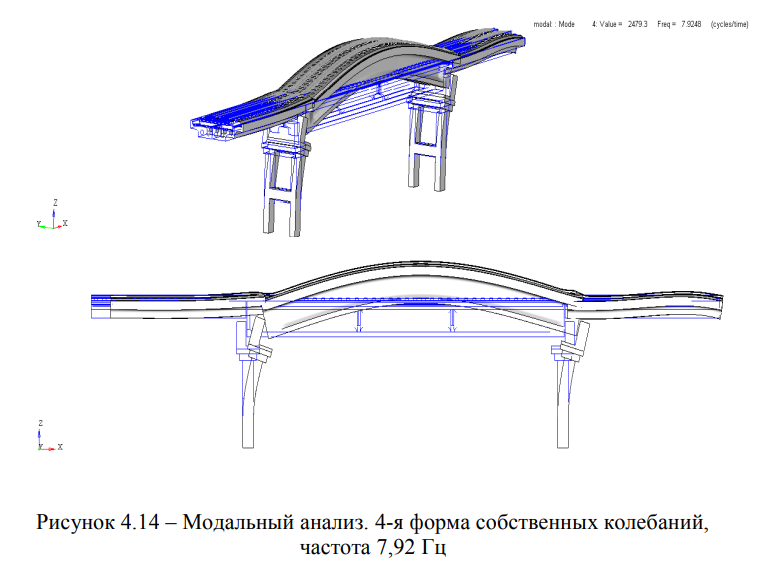
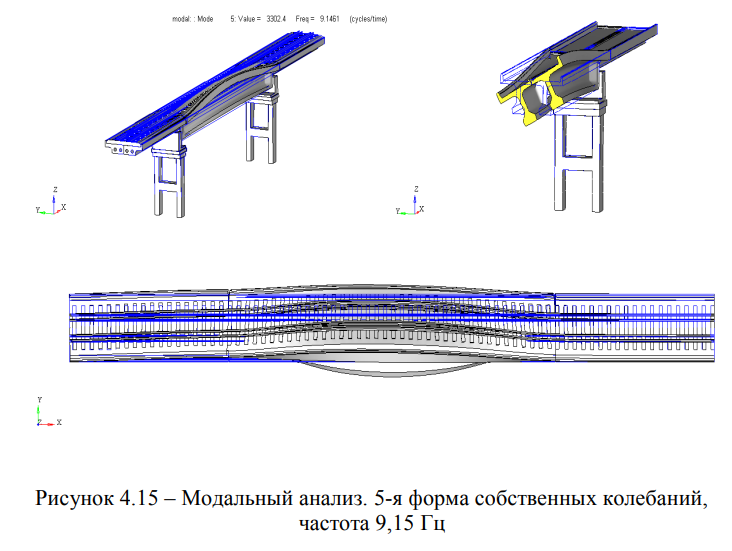
Результаты модального анализа сведены в таблицу 4.2 и представлены на рисунках 4.12 — 4.16.
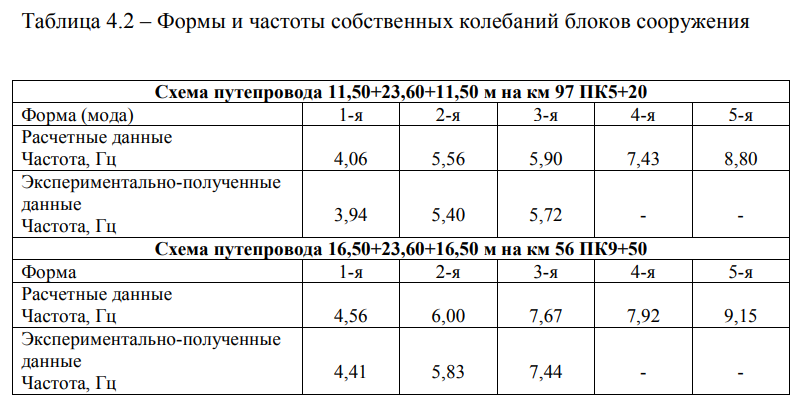
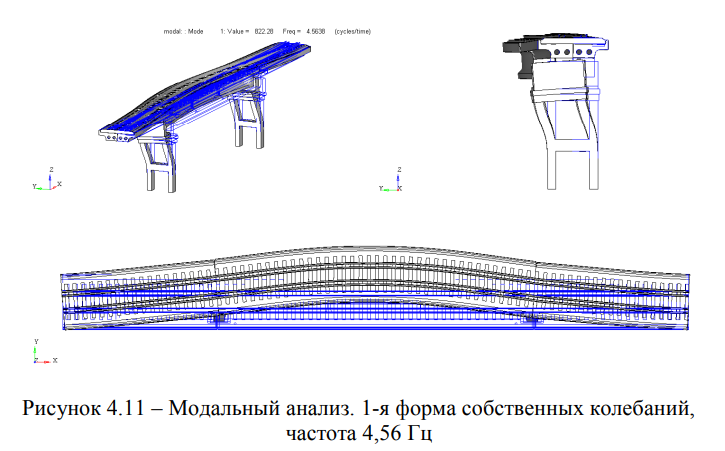
Форма 1. 1-я поперечная изгибная форма колебаний, частота 4,56 Гц (Рисунок 4.11); Форма 2. 1-я вертикальная изгибная форма, частота 6,00 Гц (Рисунок 4.12); Форма 3. 2-я поперечная изгибная форма колебаний, частота 7,67 Гц (Рисунок 4.13); Форма 4. 2-я вертикальная изгибная форма, частота 7,92 Гц (Рисунок 4.14); Форма 5. Сложная форма колебаний (одновременно крутильная и поперечная изгибная), частота 9,15 Гц (Рисунок 4.15).
Расчет металлического балочного пролетного строения
железнодорожного моста
В качестве эксплуатационной поперечной нагрузки на мост принимается подвижной состав, с известной осевой нагрузкой 24 тс на ось. Мостовое полотно состоит из двух металлических балок длиной L=27 м, соединяемые между собой диагональными связями. Предполагается, что накатывание осей тележек происходит поочередно. Опорные части — жестко соединены с опорами в поперечном направлении. Верхнее строение пути — безбалластное мостовое полотно, т.е. на деревянных поперечинах [25, 93, 94].
Сечение продольной балки — двутавр, сечение стенки двутавра размером 960*10 мм, сечение полки двутавра размером 360*14 мм. Металлоконструкция изготовлена из стали марок 15ХСНД, 15ХСНД-2, 10ХСНД, 10ХСНД-2 по [113]. Элементы и связи соединены высокопрочными болтами и сваркой.
Расчетная схема рассматриваемой системы приведена на рисунке 4.16, конечно-элементная модель (Рисунок 4.17), по аналогии [35 — 39].
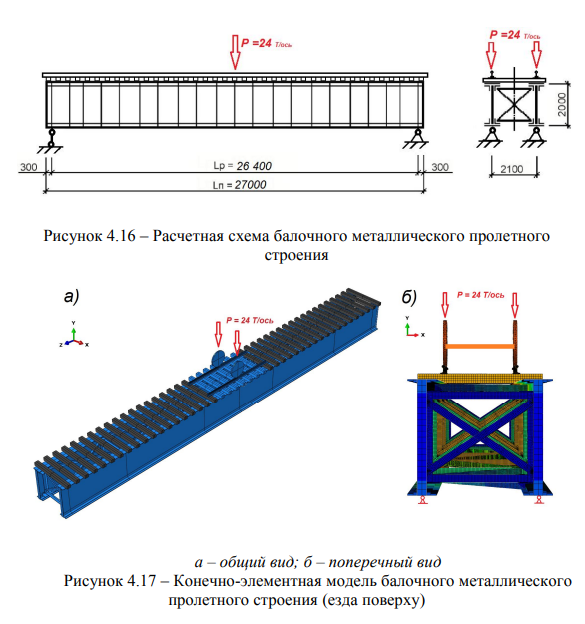
Расчет методом конечных элементов (МКЭ) выполнен с использованием программного комплекса APM Civil Engineering, версия APM WinMachine 2008 (v.9.5), проектирование и расчет металлоконструкции моста, разработанного Российским Научно-техническим центром «Автоматизированное Проектирование Машин» (НТЦ АПМ). Система ВСП (рельс Р65, деревянные шпалы) — пролетное строение — опорные части
моделировалась стержневыми элементами, работающими на продольную, поперечную силу и изгиб [47, 48].
Анализ спектров вертикальных перемещений балочных бездефектных и имеющих дефекты пролетных строений

По результатам расчетов МКЭ с достаточной точностью и минимальными временными затратами, определены собственные частоты дефектных пролетных строений, что позволило выполнить сравнение полученных расчетных данных с экспериментальными данными (Рисунки 4.18 — 4.24).
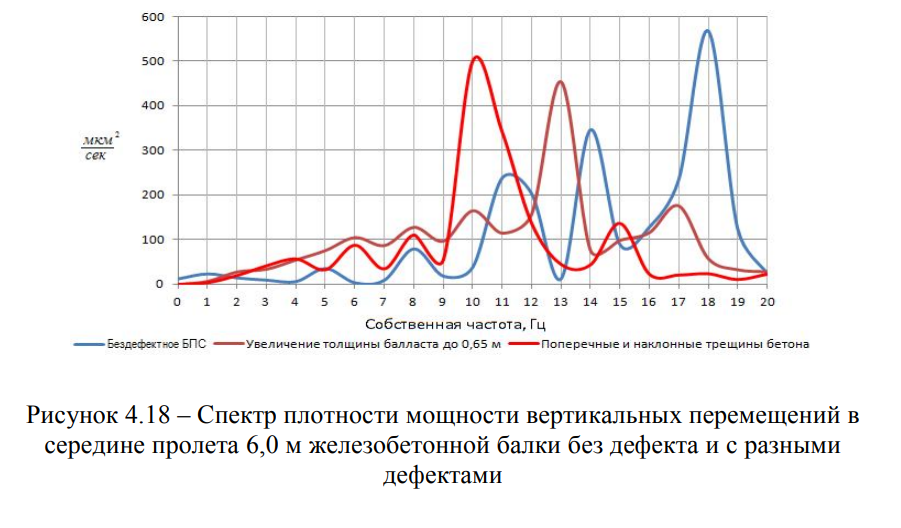
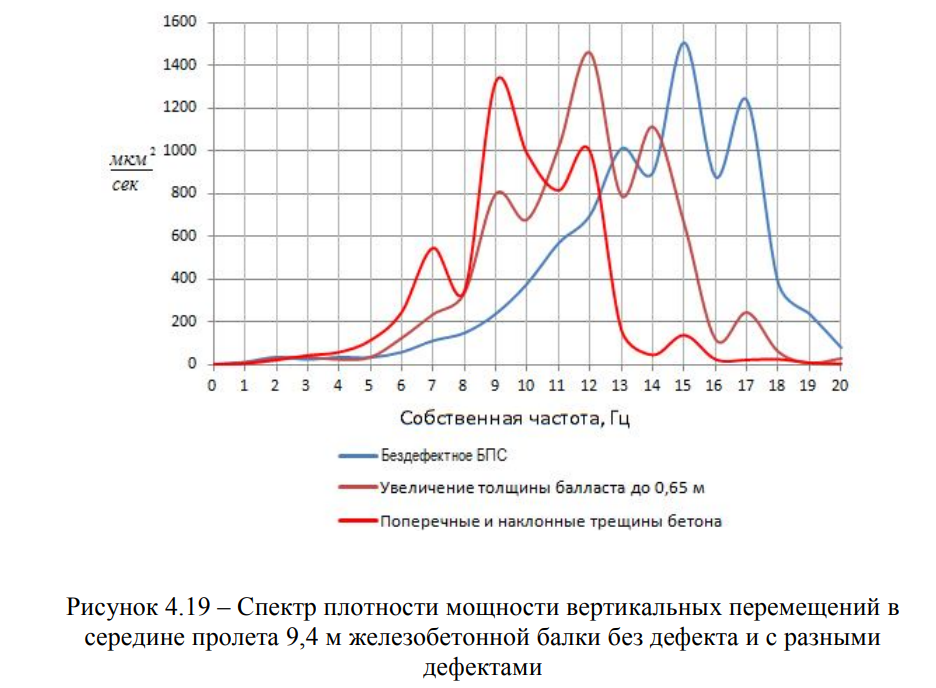
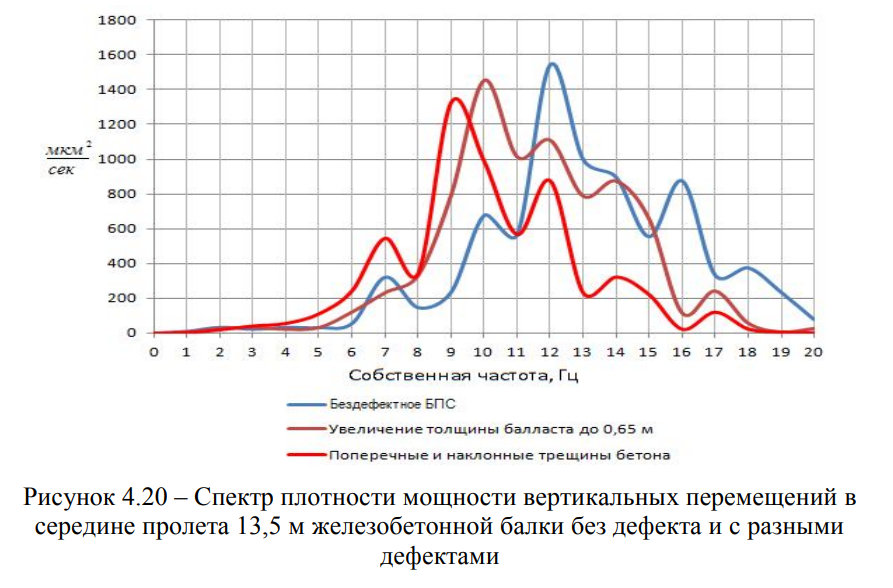
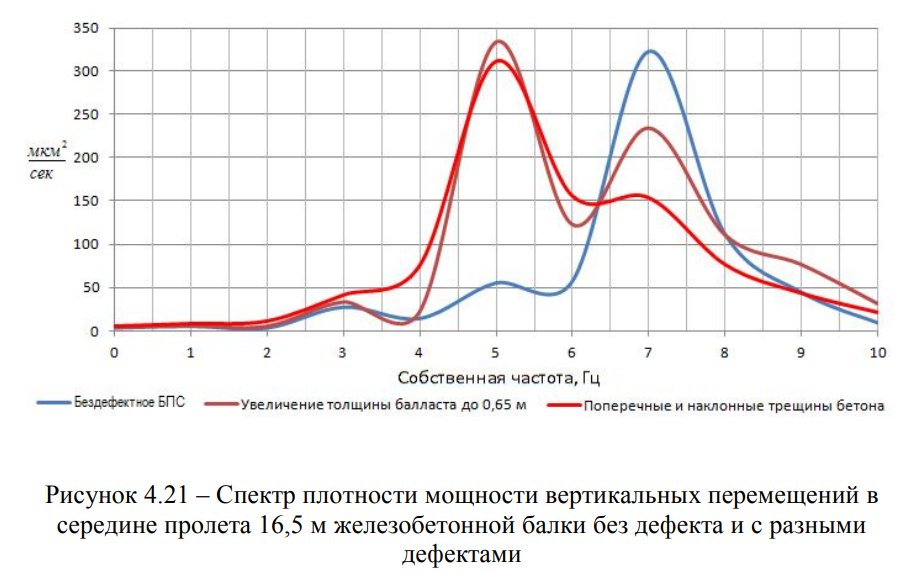
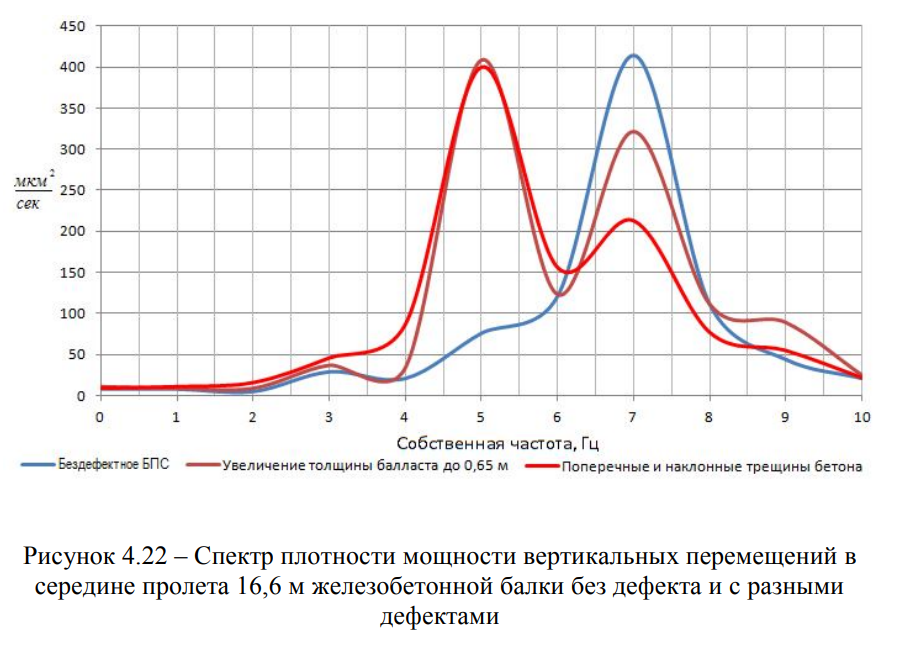
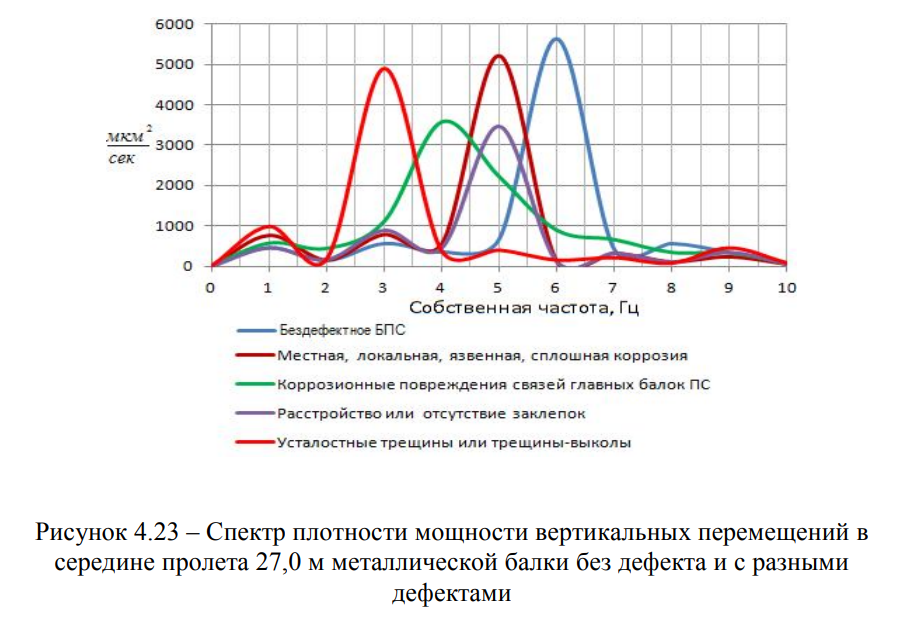
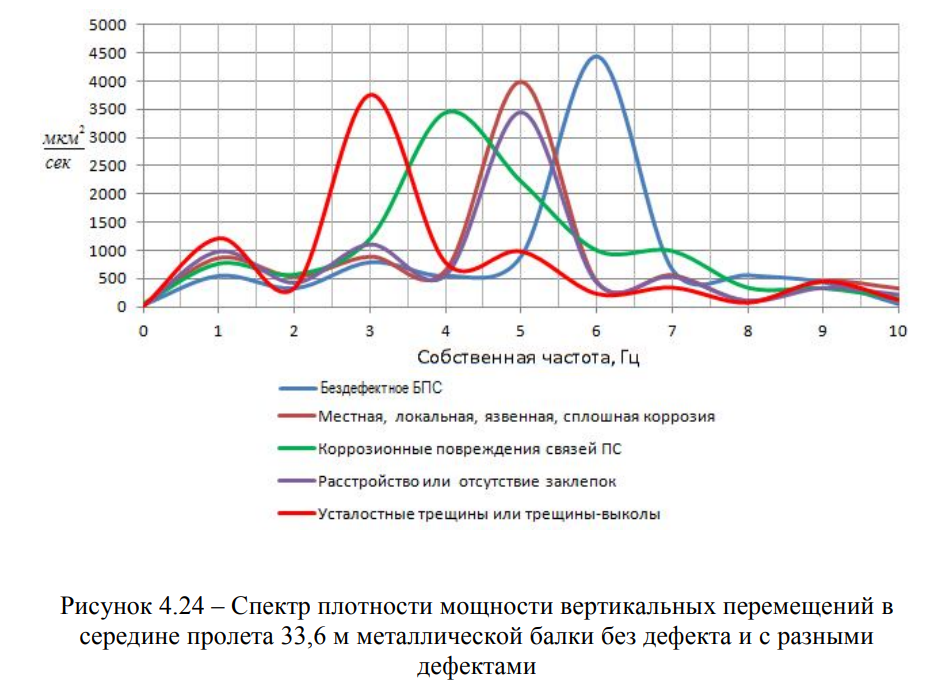

Основным вопросом, связанным с моделированием взаимодействия пролетного строения с повреждениями и проходящего по нему подвижного состава, является численное описание повреждения.
На частоту собственных колебаний ƒ, помимо жесткости самого пролетного строения, оказывает влияние масса конструкции т, которая изменяется за счет изменения толщины слоя уложенного балласта под шпалой hб.
На пролетных строениях железнодорожных мостов, для одного и того же пролета, толщина балластного слоя может изменяться значительно. В таблице 4.3 показаны расчетные значения частот собственных колебаний для железобетонных пролетных строений от 6 м до 16,6 м, бездефектных и имеющих дефекты.
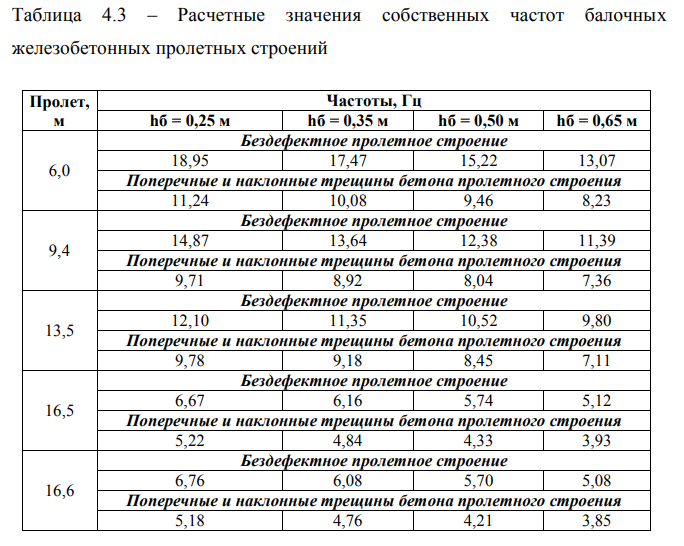
Трещины моделируются присоединением дополнительной точечной массы к балке, что приводит к снижению собственной частоты, такому же, как и при появлении трещины.
Анализ изменения собственных частот позволяет сделать следующие выводы:
- если собственная частота упала, то появилось опасное сечение;
- если для 2-ой частоты наблюдается малое падение, а для 3-ей — большое, то опасное сечение в середине балки.
- если мало падение 3-ей частоты и велико 4-ой одновременно, то опасное сечение находится на расстоянии 1/3 от одной из опор.
Частоты определены при значениях толщины слоя балласта под шпалой hб = 0,25 ÷ 0,65 м. Промежуточные значения частоты при соответствующей толщине слоя балласта под шпалой hб с могут быть определены по линейной интерполяции.
В таблицах 4.4 и 4.5 приведены расчетные характеристики железобетонных и металлических балочных пролетных строений с дефектами и без дефектов.
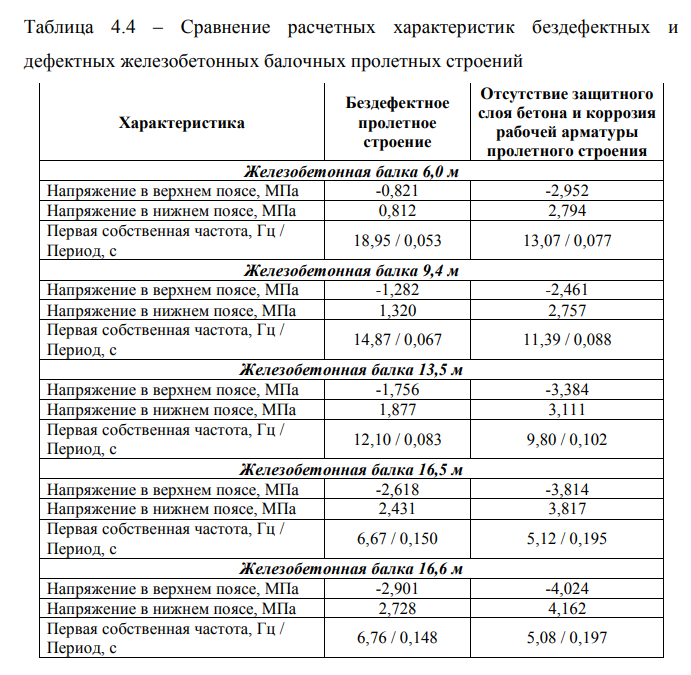
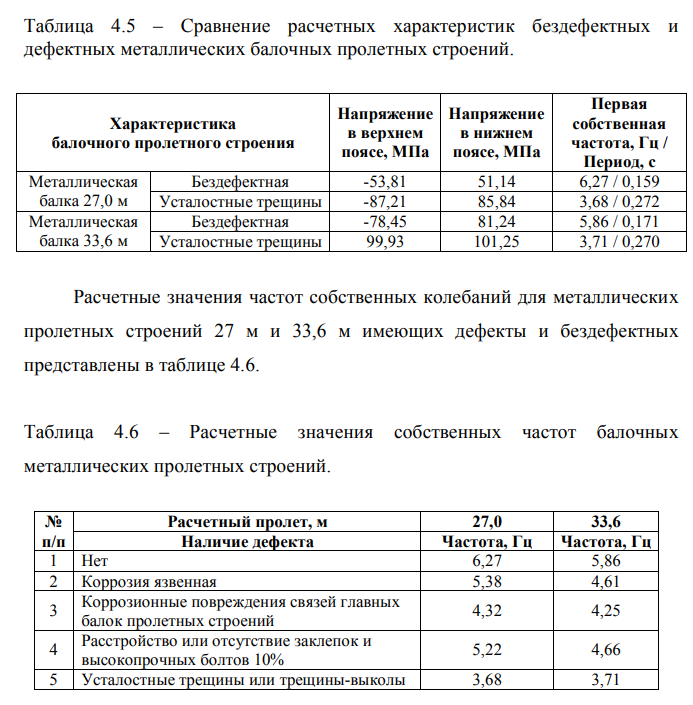
Язвенная коррозия, коррозионные повреждения связей главных балок пролетных строений, расстройство или отсутствие заклепок и высокопрочных болтов, усталостные трещины или трещины-выколы, так же моделируются присоединением дополнительной точечной массы к балке, что приводит к снижению собственной частоты, причем, чем больше точечная масса, тем значительнее дефект.
Выводы по четвертой главе
На основании результатов расчетов подтверждено положение, что включение в совместную работу с основными несущими конструкциями элементов мостового полотна и верхнего строения пути повышает точность решения задачи об определении собственных частот.
Адаптация конечно-элементной модели по результатам статических и динамических испытаний позволяет повысить достоверность расчетных значений собственных частот и напряжений возникающих в элементах конструкции железнодорожного моста.
Анализ расчетной величины первой собственной частоты позволяет сделать вывод о возможности использования первой собственной чистоты для определения наличия или отсутствия дефекта в пролетном строении.
Сравнение измеренных и расчетных значений собственных частот позволяет определить наличие повреждения в балочном пролетном строении и может служить основой методики экспресс-оценки технического состояния балочных пролетных строений эксплуатируемых железнодорожных мостов.
Список литературы
- Султан А.Е. Экспериментальные исследования воздействия малых масс на металлическую ферму железнодорожного моста / Султан А.Е., Бондарь И.С. // Сборник научных трудов профессорско-преподавательского состава и студентов посвященной 135-летию М. Тынышпаева «Транспорт в XXI веке: состояние и перспективы» — Алматы, 2016. — С. 615-619.
- Тимошенко С.П. Прочность и колебания элементов конструкций. М.: Наука — 1975. — С. 706
- Тимошенко С.П. Колебания в инженерном деле / С.П. Тимошенко, Д.Х. Янг, У. Уивер. /. М.: Машиностроение — 1985. — С. 472.
- Филиппов А.П. «Теория колебаний и задачи динамики//Прикладная механика», Киев: 1967 — Т.З, Вып.11 — С. 35-46.
- Уздин А.М., Ваничева С.С., Кузнецова И.О., Ван Хайбинь. К вопросу задания сейсмического воздействия на большие мосты применительно к мосту через Керченский пролив // Природные и техногенные риски. Безопасность сооружений. 2015, №2, с.21-26.
- Уздин А.М., Воробьева К.В., Фрезе М.В., Ван Хайбинь, Чанг Юань. Влияние взаимодействия фундамента с основанием на динамику металлических пролетных строений мостов // Основания, фундаменты и механика грунтов. 2016, №5, с.35-40.
- Хазанов М.Л. Обработка результатов динамических испытаний мостовых сооружений программой «Спектр» // Труды ЦНИИС, Вып. 208, 2002.
- Хазанов М.Л. Анализ напряженно-деформированного состояния мостовых конструкций с использованием компьютерной измерительной системы. Диссертация на соискание ученой степени кандидата технических наук — Москва — 2007. — 130 с.
- Цветков Д. Н. Оценка технического состояния сталежелезобетонных пролетных строений железнодорожных мостов по динамическим параметрам. Диссертация на соискание ученой степени кандидата технических наук — Новосибирск — 2010. — 125 с.
- Шарипбай А.Ш. Экспериментальные исследования воздействия малых масс на железобетонные балки железнодорожного моста / Шарипбай А.Ш., Бондарь И.С. // Сборник научных трудов профессорско-преподавательского состава и студентов посвященной 135-летию М. Тынышпаева «Транспорт в XXI веке: состояние и перспективы» — Алматы, 2016. — С. 620-624.
- Шапошников H.H. Применение метода конечных элементов к решению динамических задач / Шапошников H.H., Римский P.A., Полторак Г.В., Бабаев В.Б. // Расчеты на прочность. — 1986 — Вып. 27. — С. 220-237.
- Шапошников H.H. Расчет конструкций на действие подвижной нагрузки с использованием метода конечных элементов / Шапошников H.H., Кашаев С.К., Бабаев В.Б., Долганов A.A. // Строительная механика и расчет сооружений. — 1986 — №1. — С. 50-54.
- Шахтерле К. Усиление и переустройство железнодорожных мостов — М.: Трансжелдориздат, 1935 — С. 228.
- Шестериков В.И. Пути повышения долговечности эксплуатируемых мостов // Сборник научных трудов ГИПРОДОРНИИ, М.: 1986 — С. 5-15.
- Яшнов А.Н. Грузоподъемность плиты балластного корыта железобетонных пролетных строений железнодорожных мостов.
Диссертация на соискание ученой степени кандидата технических наук — Новосибирск — 1989. — 128 с. - Яшнов А. Н. Совершенстовование методики диагностики железобетонных пролетных строений по результатам исследования их динамической работы / А.Н. Яшнов, А.В. Слюсарь // Общество железобетонщиков Сибири и Урала. Научные труды. — Новосибирск, 2005. — Вып. 8. — С. 83-85.
- Abdel Wahab MM, De Roeck G, Peeters B. Parameterization of damage in reinforced concrete structures using model updating. Journal of Sound and Vibration. — 1999. — № 228(4).- рр.717-30.
- Agrati S., «Estimation of Structural Parameters from Ambient Vibration Test», Masterthesis, Danish Technical University. — 1994.
- Aktan A.E., Lee KL, Chuntavan C, Aksel T. Modal testing for structural identification and condition assessment of constructed facilities. In: Proceedings of 12th International Modal Analysis Conference. — 1994. рр. 462-468.
- Aktan A.E., «Issues in Instrumented Bridge Health Monitoring», IABSE Symposium San Francisco. — 1995.
- Aktan AE., Necati Catbas F. Modal analysis for damage identification: past experiences and Swiss Z-24 bridge. In: Proceedings of 20th International Modal Analysis Conference. — 2002. pр. 448-456.
- Bruel and Kjaer. Mechanical Vibration and Shock Measurements. 1890. — p.145.
- Chellini G., Nardini L.,Salvatore W. Dynamical identification and modeling of steelconcrete composite high-speed railway bridge, Structure and Infrastructure Engineering, — 2009. pр. 1-19.
