Цикл статей:
Глава 1 — Вибродиагностика балочных пролетных строений
железнодорожных мостов
Глава 2 — Технические средства измерений и обработки колебаний конструкций мостов
Глава 3 — Натурные эксперементальные исследования динамических воздействий на балочные пролетные строения железнодорожных мостов
Глава 4 — Расчет балочных пролетных строений
Глава 5 — Методики вибродиагностики балочных пролетных строений железнодорожных мостов
Общие характеристики балочных пролетных строений железнодорожных мостов
Объектами исследований, изложенных в настоящей главе, являлись: а) балочные металлические пролетные строения мостового перехода через канал Иртыш-Караганда железнодорожной линии Ерейментау- Экибастуз, с пролётами I = 3 х 27 м, тип полотна — на деревянных брусьях, год постройки — 1952 (Рисунок 3.1) [52, 65];
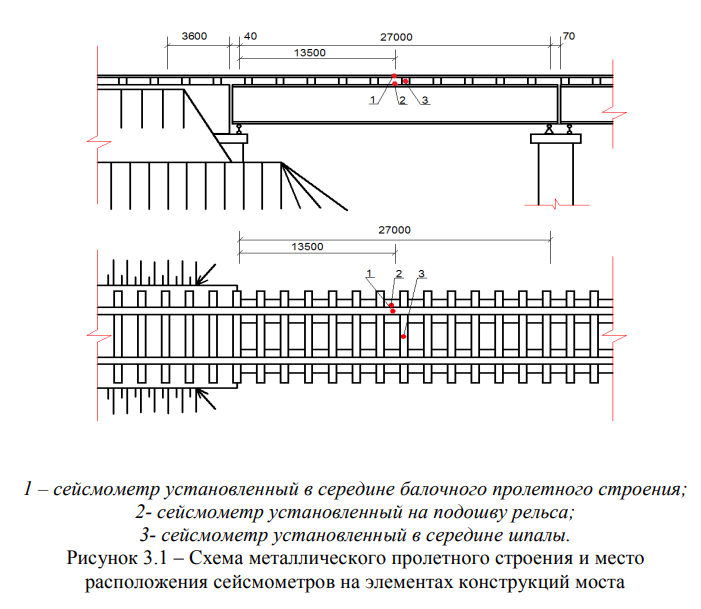
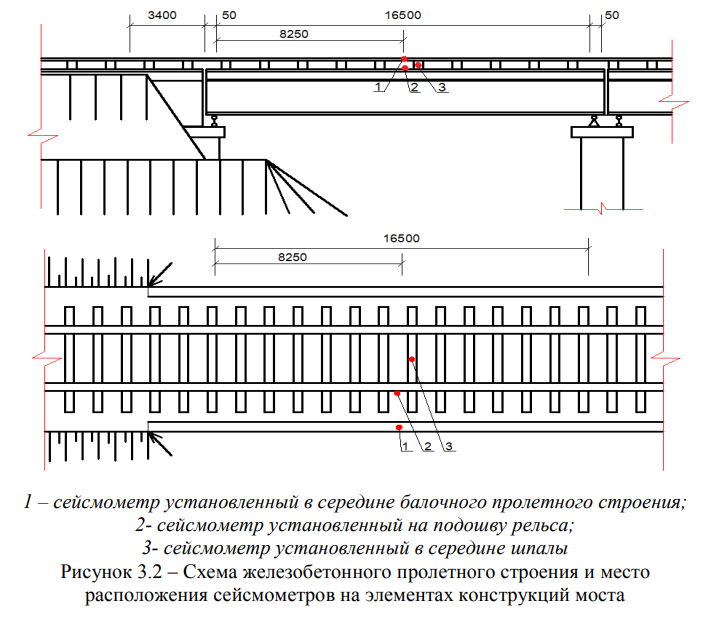
б) балочные железобетонные пролетные строения мостового перехода через канал Иртыш-Караганда железнодорожной линии Ерейментау- Экибастуз, с пролётами I = 2 х 16,5 + 27 + 2 х 16,5 м, тип полотна — на
щебеночном балласте, год постройки — 1972 (Рисунок 3.2) [52, 65]. Графики вертикальных перемещений, ускорений и скоростей колебаний пролетных строений и соответствующие им графики СПМ представлены в Приложении А;
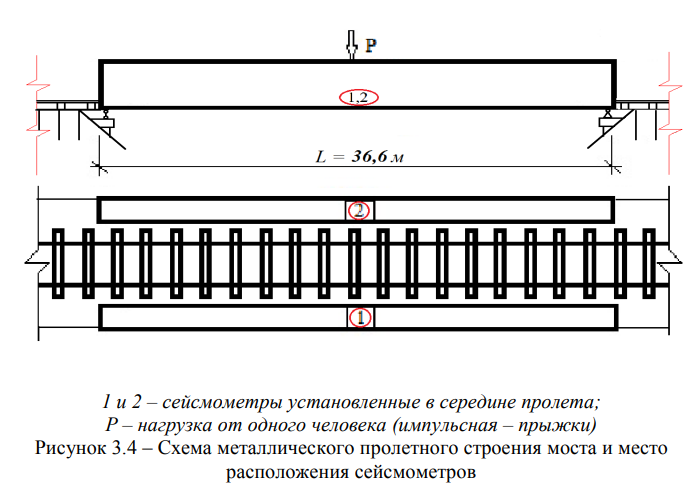
в) балочное металлическое пролетное строение железнодорожного моста через р. Сарыбулак железнодорожной линии Айнабулак-Алматы, с пролётом I = 36,6 м, тип полотна — на деревянных брусьях с ездой понизу, год
постройки — 1962 общий вид и схема представлены на рисунках 3.3 и 3.4 [74];

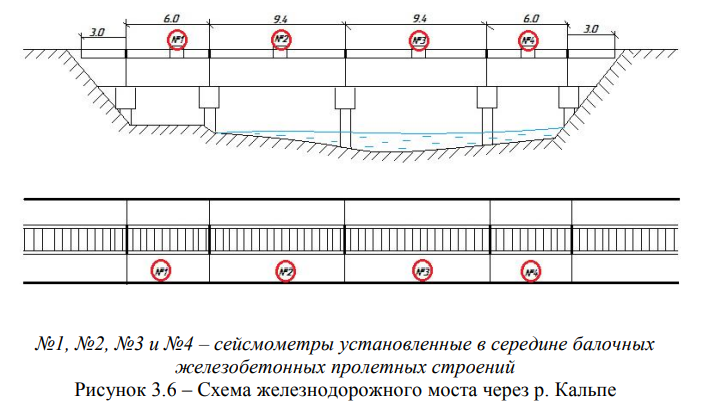
г) балочные железобетонные пролетные строения железнодорожного моста через р. Кальпе железнодорожной линии Айнабулак-Алматы, с пролётами I = 6 + 2 х 9,4 + 6 м, тип полотна — на щебеночном балласте, год
постройки — 1978. Общий вид и схема расположения сейсмометров на пролетных строениях показаны на рисунках 3.5 и 3.6 [53, 92];

д) балочное металлическое пролетное строение железнодорожного моста через р. Иртыш железнодорожной линии Семей-Алматы, с пролётом I = 27 м, тип полотна — на деревянных брусьях, год постройки — 2008. Общий
вид и схема расположения сейсмометров и тензорезисторов представлены на рисунках 3.7 и 3.8 [14, 83];

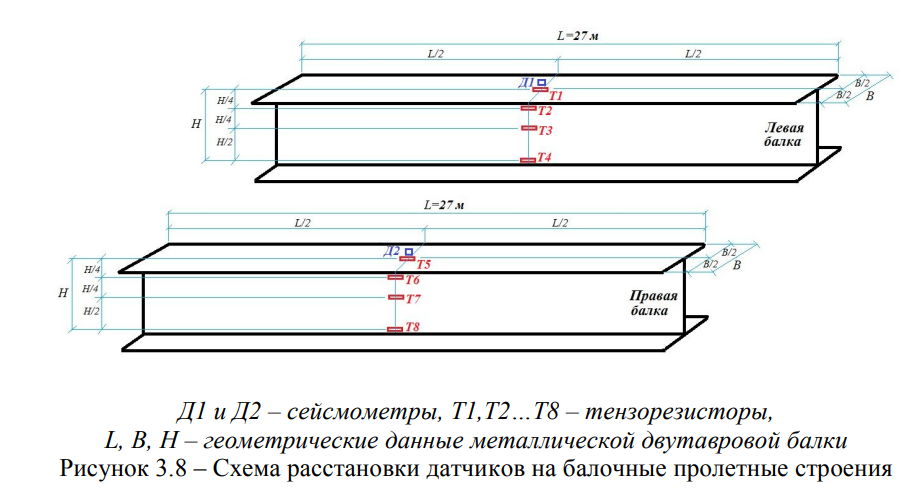
е) балочное железобетонное пролётное строение железнодорожного моста, железнодорожной линии Астана-Павлодар, с пролётом I = 2 х 6 м, тип
полотна — на щебеночном балласте, год постройки — 1939. На рисунке 3.9 приведено поперечное сечение пролетного строения с указанием мест установки тензорезисторов на элементах конструкции моста [9, 54];
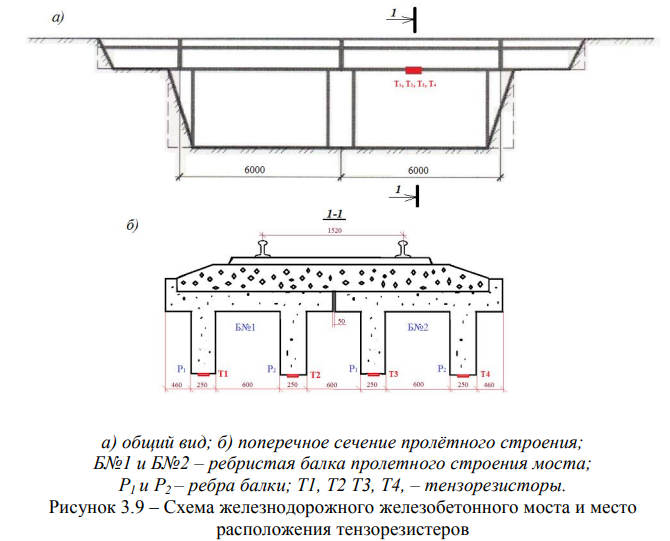
Для дальнейшего мониторинга при помощи ТПАК в осенне-зимний и весенне-летний периоды, произведена защита тензорезисторов от внешних воздействий окружающей среды [9, 54, 124].
Результаты измерений деформаций балочных пролетных строений железнодорожных мостов при воздействии подвижного состава
В качестве средства измерений использовался ТПАК с пакетом прикладных программ по обработке и визуализации данных «ТЕНЗО», технические характеристики, программное обеспечение и методика обработки сигналов достаточно подробно приведены в [9, 13, 54].
Исследования проводились в светлое время суток, в летний период, при движении подвижного состава с различными скоростями V = 41 ^ 98 км / ч .
В данном подразделе приведены некоторые результаты измерений относительных деформаций железобетонного балочного пролётного строения железнодорожного моста [12, 14] при проходе различного подвижного состава, состоящего из одной или нескольких подвижных единиц различных типов: ВЛ-80, К28А, Дрезина ДГКу, ВЛ-80 + путеизмерительный вагон, К24АТ + пять пассажирских вагонов, К24АТ- Тулпар-«Тальго», Мотор-вагонный подвижной состав (электричка), ВЛ-80 + спецтехника + вагон (рабочий поезд).
На рисунке 3.10 представлены записи диаграмм деформаций растянутой зоны в средней части пролета при проходе одиночного локомотива ВЛ-80, в прямом и обратном направлении.
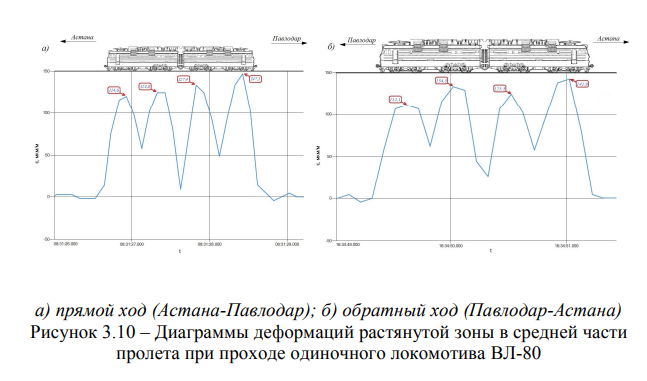
Из рисунка 3.10 можно сделать вывод, что изгибные деформации от воздействия одиночного локомотива ВЛ-80, при проходе в прямом направлении незначительно (примерно в 1,1 раз) больше чем в обратном направлении. Данное обстоятельство объясняется небольшим уклоном верхнего строения пути на мосту в прямом направлении.
Измерения произведены при 25 проходах в прямом направлении и 23 в обратном направлении. Данная тенденция прослеживается практически во всех записях. Причем максимальные изгибные деформации наблюдаются при проходе по пролетному строению второй секции локомотива. Превышение деформаций от второй секции над деформациями от первой секции составляет около 15% при движении в прямом направлении, и примерно 5,6% при движении в обратном направлении.
На рисунке 3.11 показаны записи диаграмм деформаций растянутой зоны в средней части пролета при проходе одиночного магистрального двухсекционного грузового электровоза К28А и дрезины (мотовоз) с гидромеханической передачей и подъемным краном ДГКу, в обратном направлении (Павлодар-Астана).
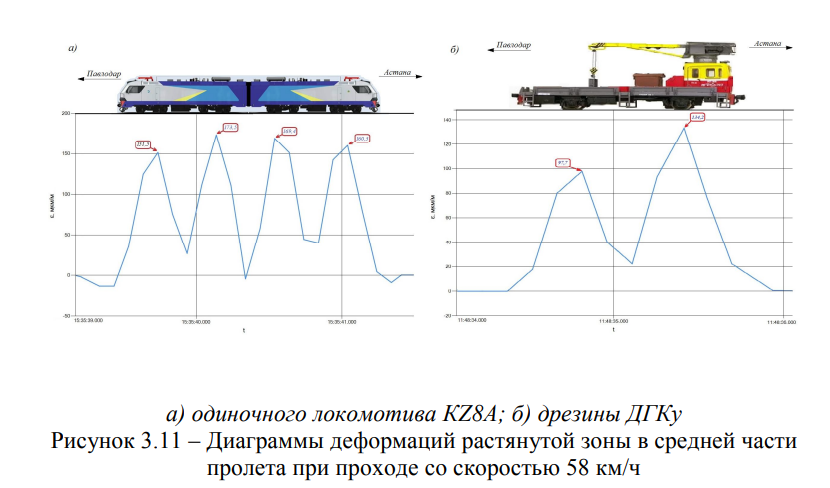
Из рисунка 3.11 видно, что максимальные деформации от воздействия при проходе одиночного локомотива К28А, в обратном направлении составляет 173,5 мкм / м, а деформации от воздействия при проходе дрезины ДГКу, в обратном направлении составляет 134,2 мкм / м. Максимальные изгибные деформации при проходе дрезины ДГКу от второй оси больше на 27,2%, чем от первой оси по ходу. Это говорит о том, что основная масса сосредоточена над второй осью дрезины ДГКу, как и показано на рисунке 3.11б. Результаты измерений изгибных деформаций балочного железобетонного пролётного строения моста под действием фактически обращаемой, на участке Астана-Павлодар, подвижной нагрузки — одиночных локомотивов и дрезины представлены в таблице 3.1.
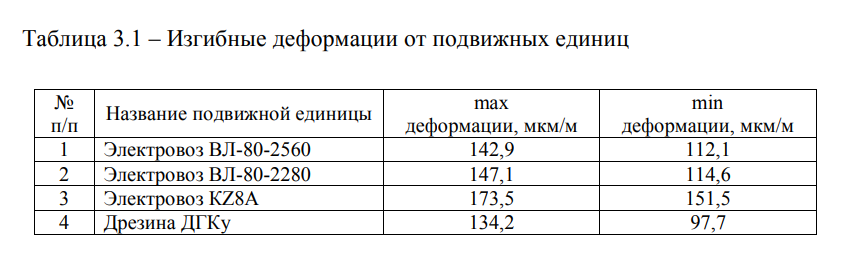
На рисунке 3.12 представлена диаграмма деформаций растянутой зоны в средней части пролета при проходе локомотива К24АТ-Тулпар-«Тальго», в прямом направлении (Астана-Павлодар).
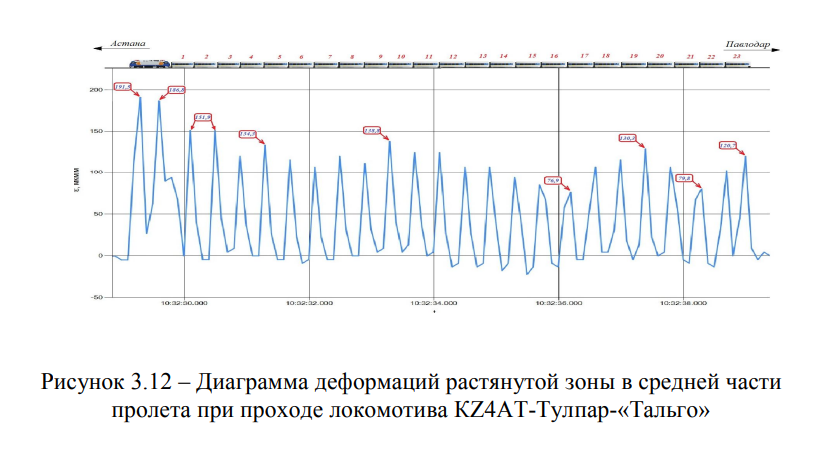
Из рисунка 3.12 видно, что изгибные деформации от воздействия магистрального пассажирского электровоза К74АТ в 1,3 раза превышают деформации от воздействия вагонов. Данное обстоятельство объясняется, прежде всего, различием баз тележек и осевых нагрузок локомотива и вагонов и, как следствие, различным характером их влияния на конструкцию. База межколесного пространства вагонов составляет 13,14 м, а база тележек электровоза К24АТ — 3,0 м соответственно.
На рисунке 3.13 показаны записи диаграмм деформаций растянутой зоны в средней части пролета при проходе локомотива К24АТ + пяти пассажирских вагонов, до и после выправки пути по мосту, в прямом направлении (Астана-Павлодар).
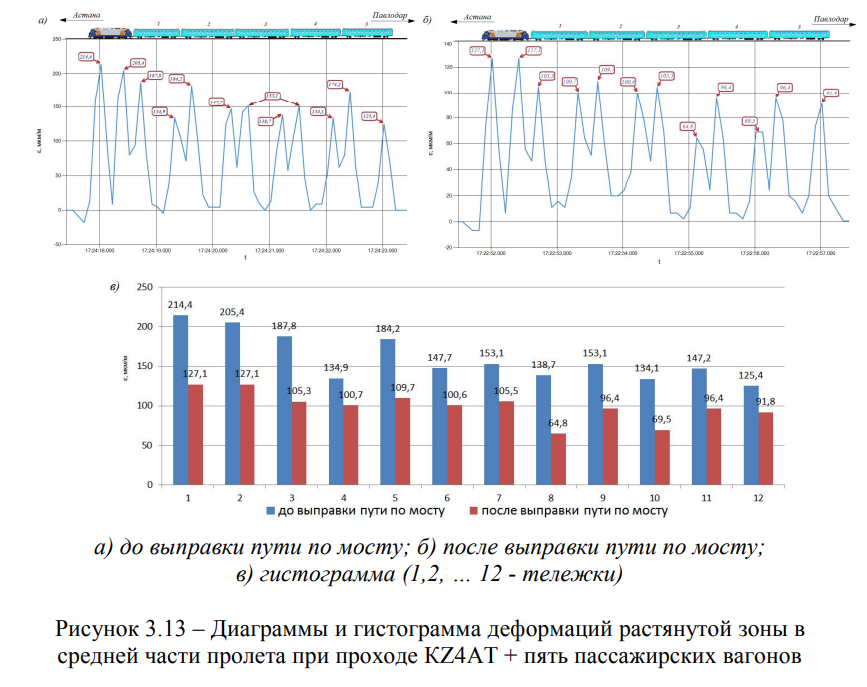
Из анализа рисунка 3.13 следует, что деформации от воздействия К74АТ + пять пассажирских вагонов, до выправки пути на мосту, в 1,69 раза превышают изгибные деформации от воздействия того же состава, после выправки пути на мосту. Данное обстоятельство объясняется, дефектом — «угон пути» и, как следствие, увеличение характера влияния на конструкцию балочного железобетонного моста.
Если сравнить обе диаграммы, то в целом можно сказать, что изгибные деформации от воздействия локомотива К74АТ до выправки пути на 12,4% больше (Рисунок 3.13а), чем после выправки (Рисунок 3.13б). Такая же ситуация наблюдается и при воздействии пассажирских вагонов, но разница составляет 14,1%. Это объясняется тем, что база тележек и осевые нагрузки от локомотива и вагонов различны. База тележек электровоза К74АТ равна 3,0 м, а база тележки четырехосных пассажирских вагонов составляет 2,7 м.
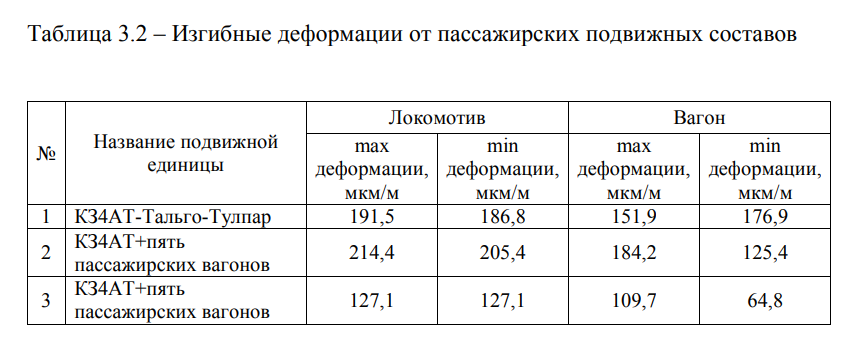
Результаты измерений деформаций балочного железобетонного пролётного строения моста под действием подвижной нагрузки К74АТ- Тулпар-«Тальго» и К74АТ + пять пассажирских вагонов, обращаемых на участке Астана-Павлодар, представлены в таблице 3.2.
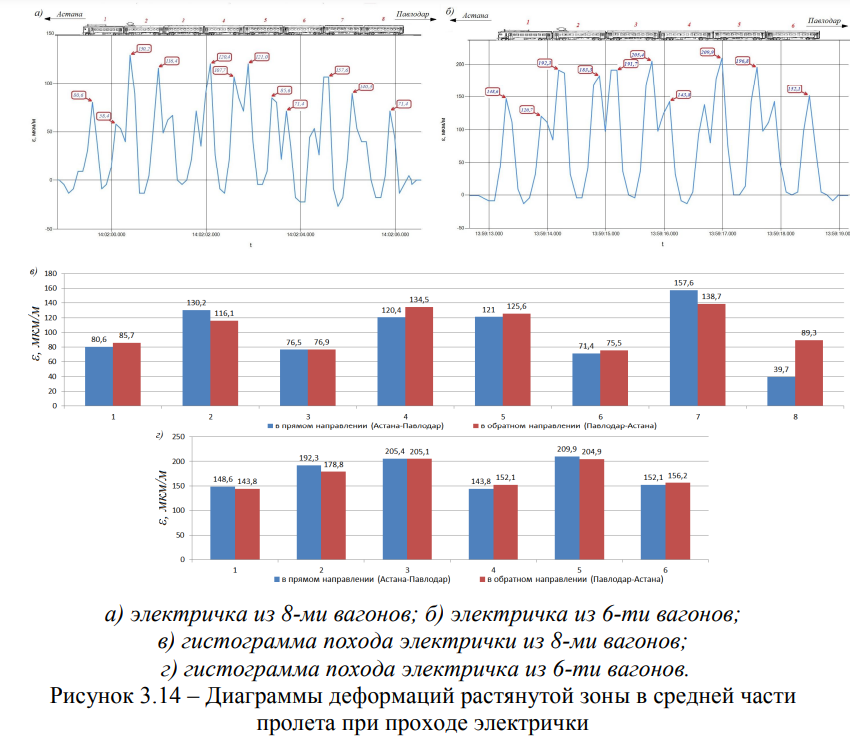
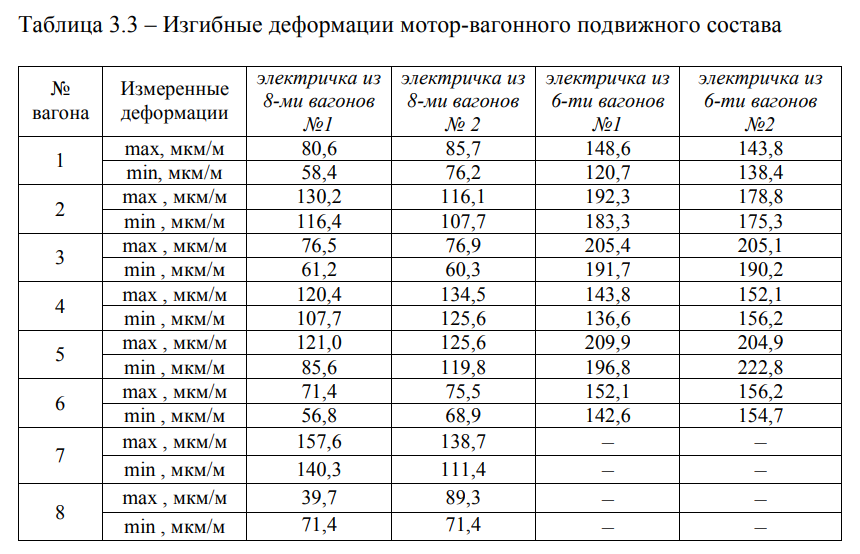
На рисунке 3.14 представлены записи диаграмм деформаций растянутой зоны в средней части пролета балочного железобетонного моста при проходе мотор-вагонного (электричка) подвижного состава из восьми
пассажирских вагонов (Рисунок 3.14а) и шести пассажирских вагонов (Рисунок 3.14б), в прямом направлении (Астана-Павлодар).
Анализ рисунка 3.14 показал, что деформации от воздействия электрички из 8-ми вагонов в 1,6 раз превышают деформации от воздействия электрички из 6-ти вагонов. Данное обстоятельство объясняется, прежде всего, скоростью и износом рессорного подвешивания части мотор- вагонного подвижного состава и, как следствие, различным характером влияния на конструкцию балочного железобетонного моста. Электричка из восьми вагонов проходила со скоростью V = 97,5 км/ч (Рисунок 3.14а), а скорость электрички из шести вагонов составила V = 83,3 км / ч (Рисунок 3.14б). Результаты измерений деформаций представлены в таблице 3.3.
На рисунке 3.15 представлена диаграмма деформаций растянутой зоны в средней части пролета при проходе ВЛ-80 + спецтехника + вагон (рабочего поезда), в прямом направлении (Астана-Павлодар) со скоростью V = 77,1 км / ч.
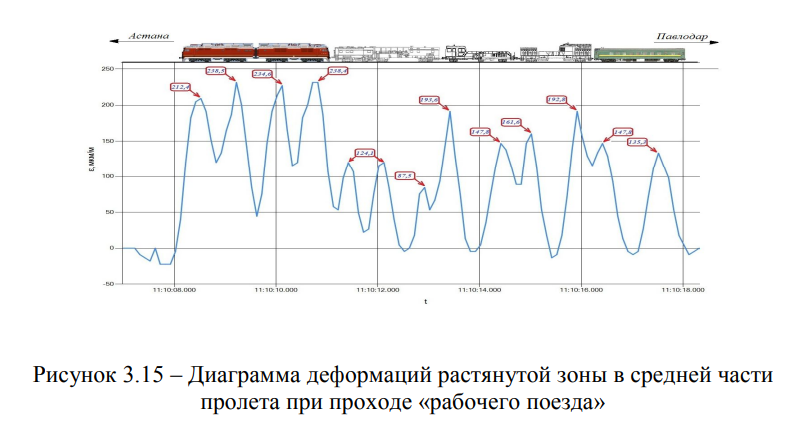
Из рисунка 3.15 видно, что набольшие деформации возникают от воздействия локомотива ВЛ-80 (238,5 мкм/м), затем от выправочно- подбивочно-рихтовочной машины (DUOMATIC) и щебнеочистительной машины (193,6 мкм / м и 192,8 мкм / м), наименьшие у пассажирского вагона
(147,8 мкм / м) и у щебнеочистительной машины (124,1 мкм / м). Это
объясняется тем, что база тележек и величин осевых нагрузок локомотива, спецтехники и вагона различны и, влияние на конструкцию балочного железобетонного моста, соответственно разное.
Выявление и анализ условий, при которых динамические деформации и перемещения в системе «МОСТ — ПОЕЗД» имеют наиболее неблагоприятный в эксплуатации характер, профессор Н.Г. Бондарь считал первостепенной задачей, подлежащей изучению в рамках проблемы взаимодействия мостов и подвижного состава [8].
От измеренных значений изгибных деформаций, зная класс бетона и расчетный модуль упругости материала конструкции, согласно закону Гука можно осуществить переход к фактическим напряжениям в конструкции моста.
Расчетные значения контролируемых параметров, таких, как напряжения в главных балках в середине пролета могут быть определены как инженерными методами, так и с помощью специализированных расчетных программных комплексов, реализующих методы конечных элементов (MIDAS Civil, APM Civil Engineering, Модуль APM Structure3D, Cosmos M). Преимущество применения конечно-элементных моделей состоит в возможности моделировать различные неисправности в конструкции, адаптируя результаты расчета к реальным условиям эксплуатации. По отклонению фактических напряжений от расчетных значений можно судить о степени поврежденности конструкций пролетного строения моста.
С целью определения изменения напряженно-деформированного состояния конструкции от воздействия климатических факторов (попеременного замораживания и оттаивания) и эксплуатируемого подвижного состава, в лаборатории имеются средства защиты установленных на конструкции тензометрических датчиков от внешних воздействий окружающей среды. Необходимо отметить, что тензометрический метод измерений деформаций и напряжений в конструкциях является наиболее точным и апробированным методом, а при определении малых деформаций при динамических воздействиях, практически единственным, и используется во всех развитых странах мира.
Периодическое проведение измерений деформаций конструкции пролетного строения в течение 2-3 лет позволит произвести прогноз изменения его состояния во времени и определить остаточный ресурс по несущей способности и грузоподъемности.
Результаты определения динамических характеристик балочных пролетных строений железнодорожных мостов
Нормами проектирования п. 1.48* [121] регламентируются частоты собственных колебаний для балочных разрезных металлических и сталежелезобетонных пролетных строений железнодорожных мостов, а также пешеходных и городских мостов.
Собственные частоты колебаний пролетного строения, регистрируемые под проходящей нагрузкой, будут существенно отличаться от расчетных частот из-за наличия в этот момент на конструкции значительной переменной массы подвижного состава. Учитывая, что погонная масса металлических пролетных строений старых норм проектирования лежит в пределах 50÷100 кН / м, а распределенная нагрузка от обращающегося в настоящее время подвижного состава может превышать 100 кН / м, зафиксировать истинные собственные частоты колебаний конструкций под движущимся поездом не представляется возможным. Поэтому собственные
частоты колебаний конструкций определяются либо по «хвостам» опытных виброграмм (осциллограмм) после ухода нагрузки с пролетного строения, либо, при необходимости проведения экспресс-диагностики, для возбуждения процесса колебаний конструкции прикладывается импульсное воздействие сосредоточенного груза малой массы в середине пролетного строения (метод малых импульсных воздействий — «прыжок человека»).
В качестве примера, на рисунке 3.16, приведены амплитудно- временная (а) и амплитудно-частотная (б) зависимости колебаний балочного металлического пролетного строения железнодорожного моста через р. Сарыбулак железнодорожной линии Айнабулак-Алматы пролётом 33,6 м, полученные при малом импульсном воздействии от прыжка одного человека весом 80-90 кг [74], где s — перемещение, мкм; t — время, с; |Sk|- модуль спектральной плотности перемещения, мкм/сек; fk — частота, Гц.
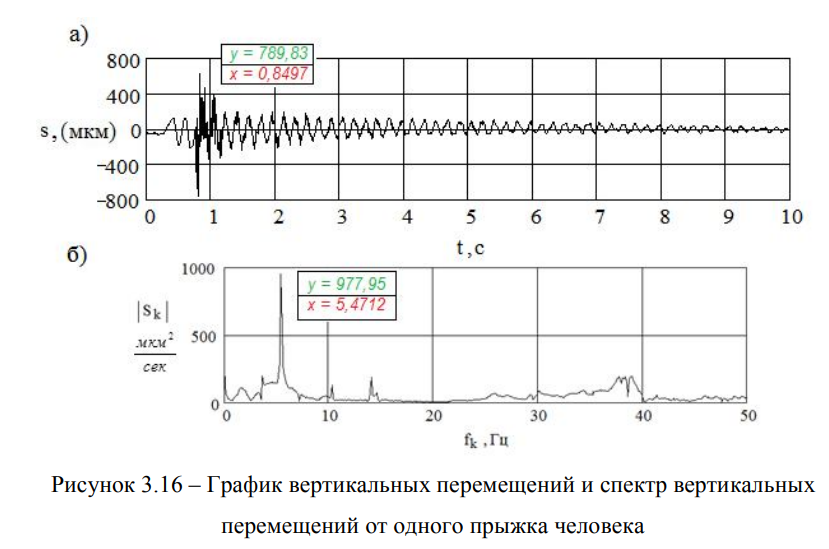
Методы определения собственных частот колебаний балочных пролетных строений по «хвостам» опытных виброграмм и малым импульсным воздействиям, апробированы, и широко применяются в практике диагностики железнодорожных мостов специалистами ОАО ЦНИИС [125], МАДИ [89] и СГУПС [91].
Виброграммы собственных колебаний записывают с помощью специальных высокочувствительных сейсмометров, входящих в состав измерительно-вычислительного комплекса для динамических испытаний конструкций, устанавливаемых в середине пролета на верхнем (или нижнем) поясе одной из металлических балок. Уменьшение собственных частот колебаний может служить показателем технического состояния конструкции, что подтверждено натурными измерениями параметров колебаний более 28 искусственных сооружений.
Результаты измерений, выполненных с применением вышеуказанных комплексов, могут визуализироваться в виде графиков изменения деформаций и напряжений (в случае известного фактического модуля упругости материала), диаграмм прогибов, амплитудно-временных и амплитудно-частотных зависимостей перемещений, скоростей и ускорений колебательного процесса, а также сохранены в цифровом виде в базе данных.
Полученные характеристики, могут служить исходными данными, повышающими точность вычислений для расчетов искусственных сооружений на сейсмостойкость, а также при динамических расчетах на устойчивость для перспективных нагрузок и при разработке модели сооружения, формировании алгоритмов задач по выявлению дефектов.
Полученные результаты натурных экспериментальных научных исследований автора опубликованы в изданиях, включенных в перечень рецензируемых журналов, рекомендуемых ВАК и в сборниках материалов Международных научно-практических конференций, в которых автор принимал личное участие и выступал с докладами, изданными в России и Казахстане [13, 14, 52, 53, 54, 74, 83, 92].
Определение амплитудно-частотных характеристик балочных пролетных строений
Особый интерес при проведении исследований представляли, как функции виброскоростей, виброперемещений и виброускорений, так и амплитудные спектры Фурье [1, 2, 66, 80, 81, 112].
В качестве примера, в ПРИЛОЖЕНИИ А приведены функции виброскоростей, виброперемещений, виброускорений и соответствующие им амплитудные спектры Фурье металлического пролетного строения — при проходе электрички из десяти вагонов со скоростью V = 98 км / ч, железобетонного пролетного строения — при проходе электрички из 8 вагонов со скоростью V = 62 км / ч .
Анализ опытных данных, характеризующих динамическую работу мостов, позволил установить параметры свободных колебаний незагруженных пролетных строений.
Определение частот свободных колебаний балочных пролетных строений
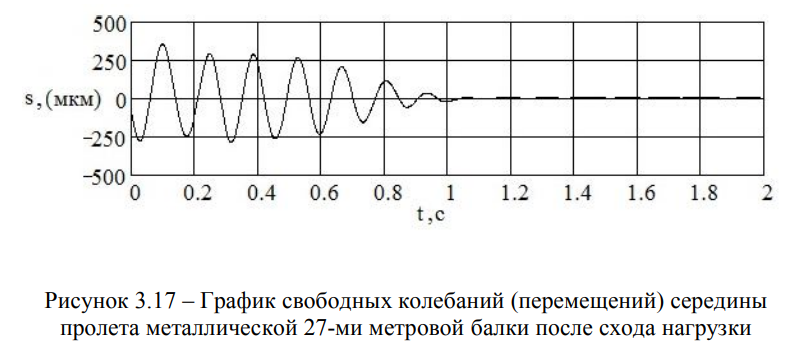
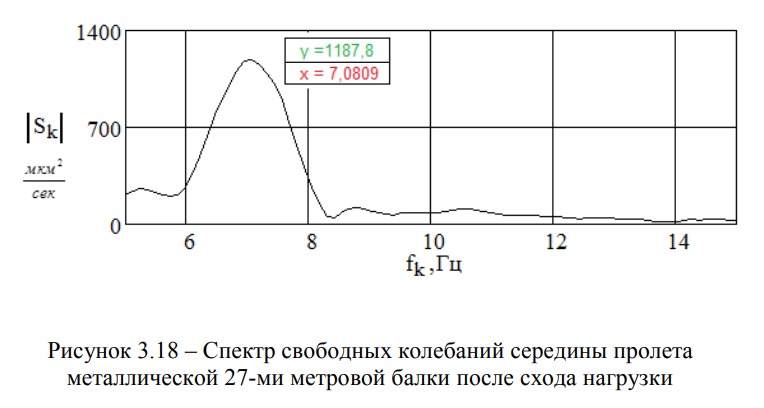
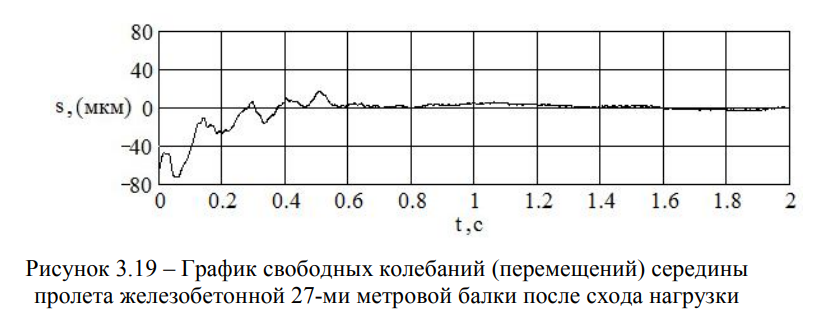
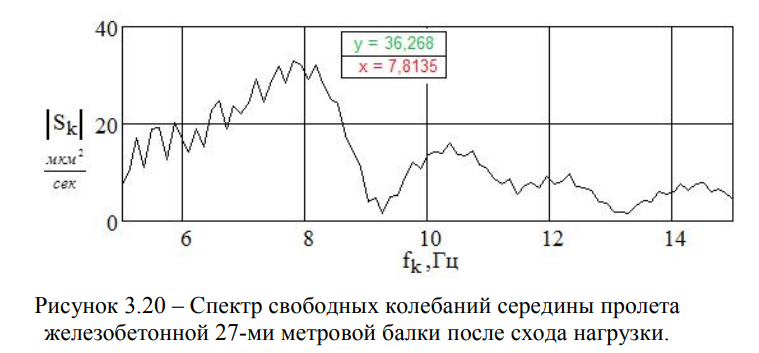
По «хвостам» опытных осциллограмм, полученных после схода поездов (Рисунки 3.17 и 3.19), и построенным по ним спектрам ответов (Рисунки 3.18 и 3.20), были определены амплитудно-временные и амплитудно-частотные зависимости.
Для мостовых переходов через канал Иртыш-Караганда железнодорожной линии Ерейментау-Экибастуз, металлического с пролётами I = 3х27 м, тип полотна — на деревянных брусьях (Рисунок 3.1) и железобетонного с пролётами I = 2 х 16 + 27 + 2 х 16 м, тип полотна — на щебеночном балласте (Рисунок 3.2), они находятся в близком частотном диапазоне fмeт = 7,08 ± 0,35 Гц и fж/б = 7,81 ± 0,39 Гц .
В результате анализа испытаний определено, что взаимодействие металлического балочного пролетного строения с подвижным составом проявляется, в основном, при возмущениях, частоты которых находятся в диапазоне f = 5,34 ÷ 7,27 Гц, а железобетонного — в диапазоне f = 5,26 ÷ 7,82 Гц .
Эти возмущения и определяют, в первую очередь, реакцию пролетных строений. Возмущения, частоты которых не попадают в эти области, как следует из анализа спектров, не играют особой роли в формировании поведения пролетных строений, так как их амплитуды очень малы и вносимая ими энергия в систему незначительна.
Определение коэффициента относительного демпфирования металлических и железобетонных балочных пролетных строений мостов
При динамических расчётах, формы спектральных кривых в области резонансов позволяют определить такую характеристику сооружения, как модальный относительный коэффициент демпфирования. Напомним, что относительный коэффициент демпфирования равен отношению реального демпфирования к критическому демпфированию.
В настоящее время в нормативных документах по расчёту сооружений на сейсмические воздействия регламентируется и используется именно
относительный коэффициент демпфирования, а не логарифмический декремент колебаний.
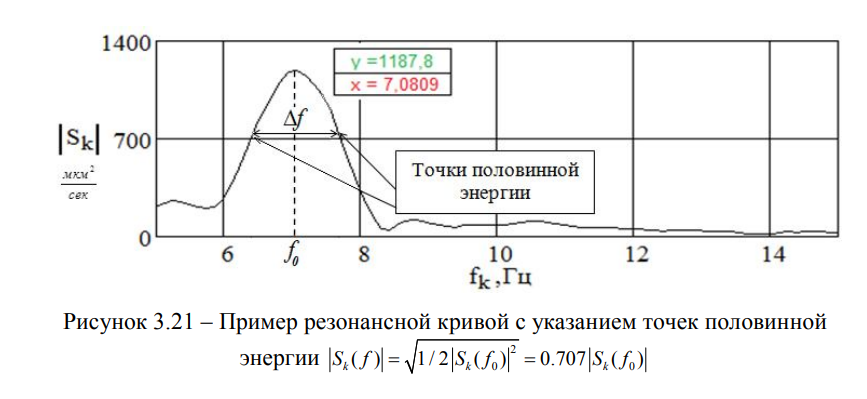

Этот параметр является модальным коэффициентом демпфирования, соответствующим данной частоте и форме собственных колебаний. Интервал частот между точками половинной энергии часто называют шириной спектра системы. Ширина интервала между точками половинной энергии определяет свойство системы рассеивать энергию при колебаниях. Увеличенная ширина интервала между точками половинной энергии может свидетельствовать о наличиии трещин в бетоне, хотя это не единственная причина [104].
Например, относительный коэффициент для железобетонных балок без трещин составляет 3%, при наличии трещин — составляет 5 ÷ 7%. Для металлической балки получен широкий спектр в области резонансной частоты, равный 7% , что свидетельствует о том, что рассеяние энергии происходит не только в пролётном строении (в металле и в соединениях
элементов балки), но и при взаимодействии с опорами и верхним строением
пути:

Анализ собственных частот колебаний балочных пролетных
строений при импульсном воздействии малых масс
В качестве средства измерений использовался ВПАК с программой по обработке и визуализации данных «ДИНАМИК», технические характеристики, методика обработки сигналов достаточно подробно приведена в [49].
Особый интерес при проведении исследований представляют, как функции, так и амплитудные спектры Фурье [8], полученные от воздействия на конструкцию пролетного строения моста в результате прыжков одного человека в середине пролетного строения.
В качестве примера, на рисунках 3.22 и 3.24 приведены функции вертикальных перемещений балочного металлического пролетного строения пролётом I = 33,6 м моста через р. Сарыбулак (место расположения сейсмометров №1 и №2 показаны на Рисунке 3.4) — при одном и пяти прыжках, а на рисунках 3.23 и 3.25 — соответствующие им графики спектральной плотности.
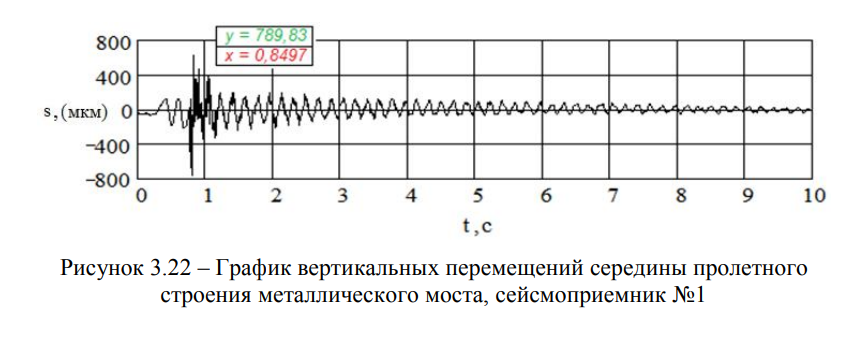
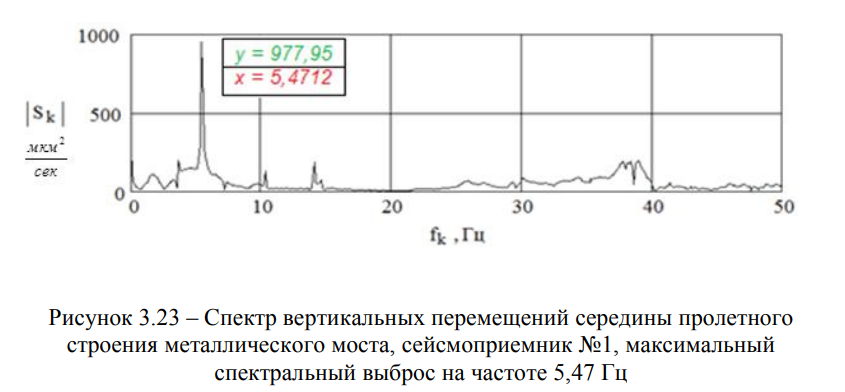
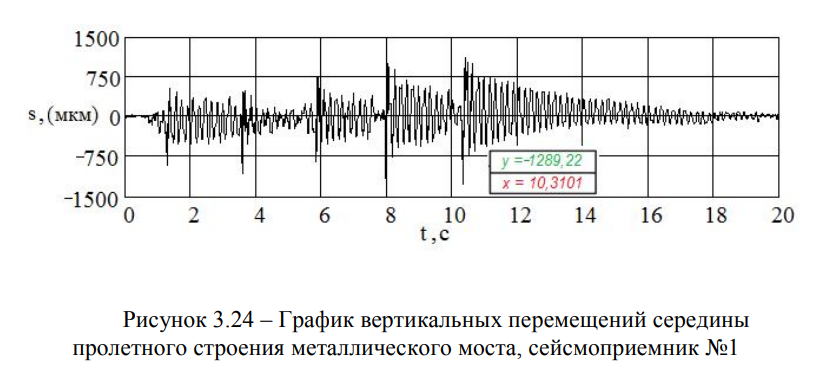
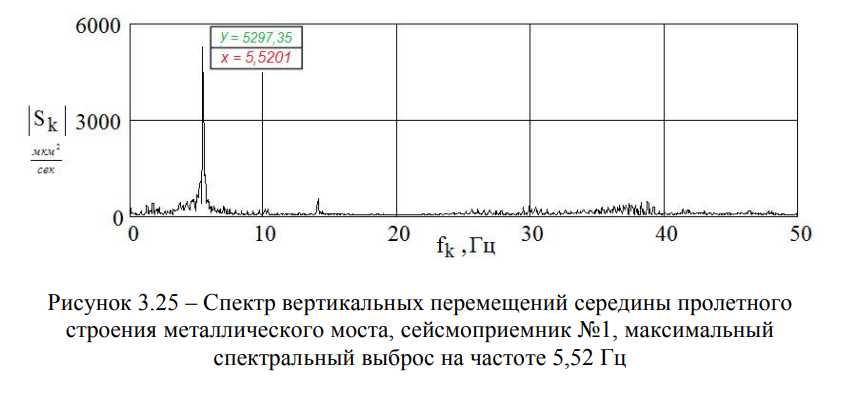
Экспериментальные данные, полученные в ходе испытаний балочного металлического пролетного строения I = 33,6 м, представлены в таблице 3.4.
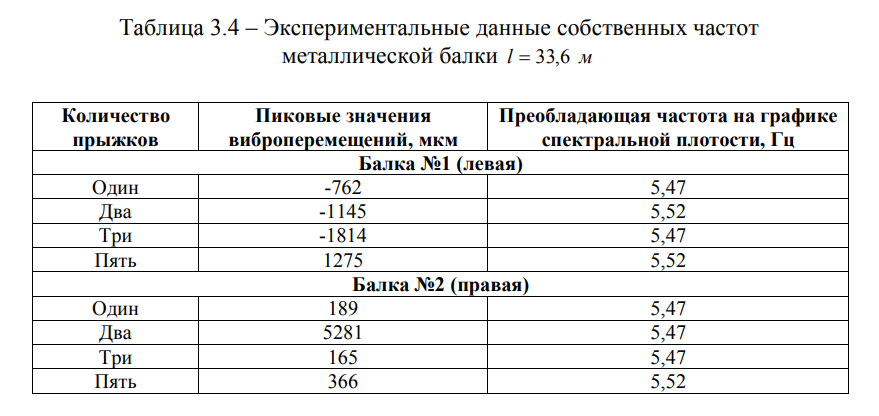

Анализ опытных данных, характеризующих отклик конструкции на воздействие малых масс (прыжков человека), позволил установить параметры свободных колебаний незагруженных пролетных строений. Преобладающие частоты на графике спектральной плотности дисперсии идентичны, независимо от количества прыжков, то есть от частоты воздействия, если время между прыжками соответствует полному затуханию колебаний.
Рассмотрим динамические испытания балочного железобетонного моста, езда поверху, расчетная схема 6,00+2*9,40+6,00 м (Рисунок 3.6), через канал Кальпе. В качестве средства измерений использовались сейсмометры (Рисунок 3.26), ВПАК с программой «ДИНАМИК» (Рисунок 2.15).

В качестве примера, на рисунках 3.27 и 3.29 приведены графики вертикальных перемещений 6-ти и 9-ти метрового балочного железобетонного пролетного строения — от пяти прыжков, а на рисунках 3.28 и 3.30 — соответствующие им графики спектральной плотности [83].
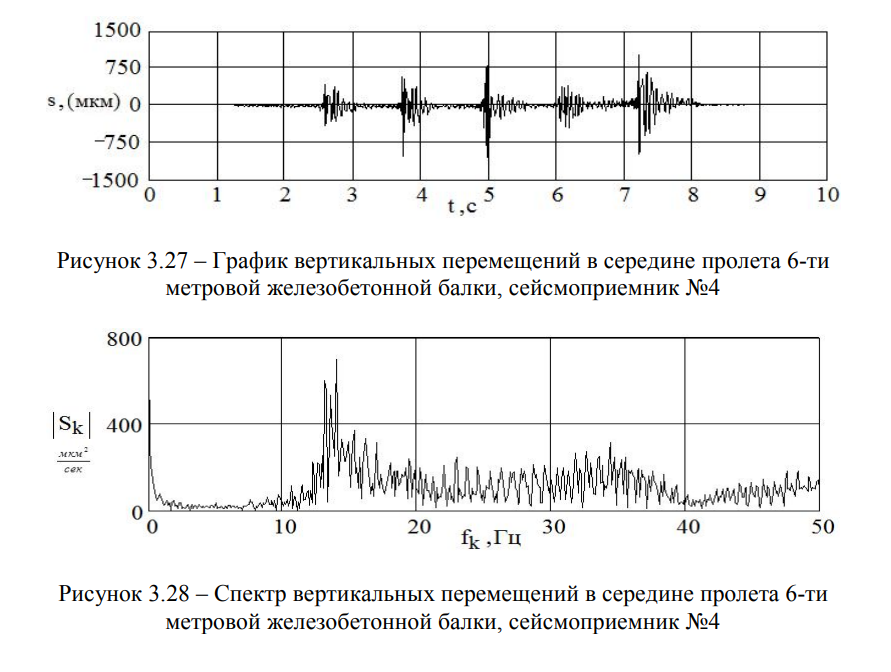
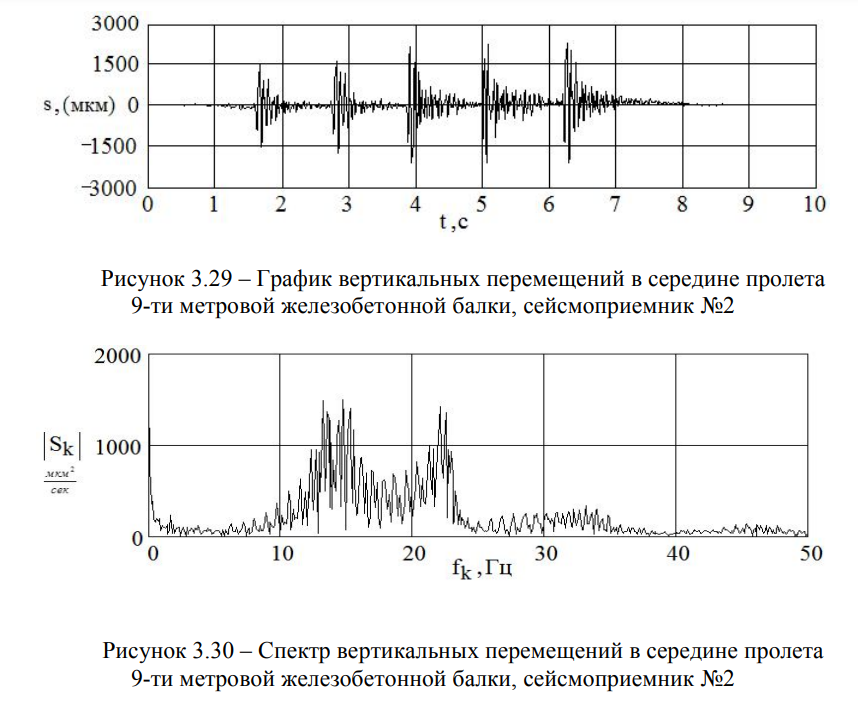

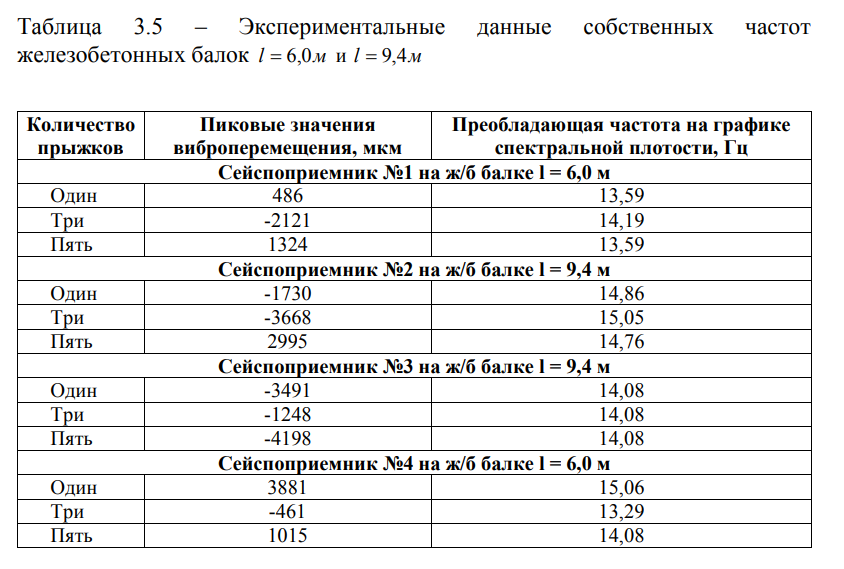
Анализ опытных данных, характеризующих отклик конструкций мостов, позволил установить параметры собственных колебаний незагруженных пролетных строений [101, 106].
По собственным колебаниям балочных пролетных строений железнодорожных мостов от малого импульсного воздействия и от воздействия любых проходящих поездов можно сделать вывод, что частоты собственных колебаний конструкций близки по численным значениям. Такая же ситуация наблюдается и при определении коэффициента относительного демпфирования. Расхождения между количественными величинами не превышают 5 % для частот собственных колебаний и 7% для коэффициента относительного демпфирования, что вполне допустимо для подобного рода исследований. Результаты вибродиагоностики, основанные на измерениях от малого импульсного воздействия, близки по значениям результатам, полученным при вибродиагностике от воздействия любой подвижной нагрузки.
Выводы по третьей главе
Из анализа натурных измерений процессов колебаний балочных пролетных строений следует, что спектр колебаний балочных пролетных строений при взаимодействии с движущимся поездом является многомодальным. При этом, частота отдельных составляющих существенно зависит от скорости движения поезда, а основная доля энергии процесса колебаний приходится на гармоники, соответствующие частотам собственных колебаний системы «СОСТАВ — ПУТЬ — МОСТ».
Для оценки состояния пролетных строений следует использовать ширину спектров в точках половинной энергии спектральной кривой в области резонансов. Сопоставляя ширину полученных спектров со спектрами новых неповрежденных пролетных строений можно оценить техническое состояние элементов конструкций.
Полученные характеристики колебаний системы «МАЛЫЙ ИМПУЛЬС (ПРЫЖОК) — ПУТЬ — МОСТ» могут служить исходными данными при калибровке модели сооружения и при составлении алгоритмов задач выявления повреждений.
Кроме того, по измеренным относительным деформациям и напряжениям в элементах конструкций от воздействия подвижного состава, можно выявлять дефекты, как в металлических, так и в железобетонных балочных пролетных строениях железнодорожных мостов.
Техническое состояние балочных разрезных металлических и железобетонных пролетных строений также характеризует коэффициент относительного демпфирования, который возрастает при наличии дефектов, влияющих на несущую способность сооружения.
Список литературы
- Квашнин М.Я. Вибродиагностика подходной насыпи железнодорожного моста / Квашнин М.Я., Косенко С.А., Бондарь И.С. / «Вестник СГУПС». — Новосибирск, 2017. — С. 34-39.
- Квашнин М.Я. Мониторинг воздействия подвижного состава на балочные пролетные строения железнодорожных мостов / Квашнин М.Я., Бондарь И.С., Жангабылова А.М. // Материалы международной научно-практической конференции «Транспортная наука и инновации», посвященной посланию президента РК Н.А.Назарбаева «Н^рлы жол — путь в будущее» — Алматы, 2015. — С. 275-279.
- Квашнин М.Я. Идентификация дефектов в балочных железобетонных пролетных строениях мостов / Квашнин М.Я., Бондарь И.С., Алдекеева Д.Т. // Сборник научных трудов VII Международной научно-практической конференции «Автомобильные дороги и транспортная техника: проблемы и перспективы развития» КазАДИ им. Л.Б. Ганчарова. — Алматы, 2019. — С. 67¬72.
- Квашнин М.Я. Экспериментальные исследования конструкций железнодорожных мостов, усиливаемых композитным материалом / Квашнин М.Я., Бондарь И.С., Рыстыгулов П.А., Кыстаубаев С.Б. // Труды Шестнадцатой научно-практической конференции «Безопасность движения поездов». — М: МГУПС (МИИТ), 2015. — Т II, С. 43-47.
- Козьмин Ю. Г. и др. Проектирование мостов и труб. Металлические мосты. — М: Маршрут, 2005. — 459 с.
- Козьмин Ю.Г., Доильницын А.Г. Расчет балочных металлических пролетных строений мостов со сквозными главными фермами. Ленинград, ЛИИЖТ, 1983. — 80 с.
- Козьмин Ю.Г. и др. Пролетное строение металлического моста с бесстыковым путем. Патент на изобретение № 2098544 от 13.12.1995г.
- Конашенко С.И. К вопросу о вынужденных колебаниях простой балки при равномерном движении по балке силы и группы сил // Сб. науч. тр. ДИИТ. — 1956. — Вып. 25. — С. 275-300.
- Косенко С.А. Эксплуатационные измерения напряжений в рельсе при воздействии подвижного состава / Косенко С.А., Квашнин М.Я., Бондарь И.С., Акимов С.С. «Известия Транссиба». — Омск, 2017. — №2(30) С. 133-145.
- Круглов В.М. и др. Методика оценки и условий использования усталостного ресурса типичных простейших строений ГИПРОТРАНСА // Транспортное строительство. — 2008.- № 7. — С.11-15.
- Курбацкий, Е.Н. Реализация дискретного преобразования Фурье при решении краевых задач теории упругости // Деп. в ВИНИТИ.- № 3267-В87.
- Курбацкий, Е.Н. Определение критических скоростей и критических сил при движении постоянной силы по балкам на упругом основании / Курбацкий Е.Н., Нгуен Ч.Т. // Известия вузов. Строительство.-2014.- № 5. С. 109-117.
- Курбацкий, Е.Н. Метод решения задач строительной механики и теории упругости, основанный на свойствах изображений Фурье финитных функций: дис. д.т.н.: 05.23.17 /Е. Курбацкий.-Москва., 1995.- 205 с.
- Курбацкий, Е.Н. Использование теоремы взвимности для оценки уровней вибраций поверхности упругого полупространства от точечного источника, расположенного внутри полупространства // Вестник МИИТа, 2004. -вып.11.
- Курбацкий Е.Н. Исследование отклика балочных мостов на воздействие поезда / Курбацкий Е.Н., Бондарь И.С., Квашнин М.Я. / «Мир транспорта». — М: МИИТ, 2015. — Том 13 №3. — С. 58-71.
- Менли Р. Анализ и обработка записей колебаний — М.: 1972 — С. 137.
- Новак Ю.В. Оценка технического состояния железобетонных мостов методами динамической диагностики / Новак Ю.В., Звягинцев А. Н., Павлов Е.И. // Научные труды ОАО ЦНИИС. — М.: 2006 — Вып. 234. — С. 29-36.
- Павлов Е.И. Разработка и развитие измерительной системы для испытаний строительных сооружений в лаборатории вибродинамических испытаний // Научные труды ОАО ЦНИИС, Вып.234. М.: 2006. — С. 55-71.
- Павлов Е.И. Динамические испытания строительных материалов, конструкций и сооружений / Е.И. Павлов, А.Б. Ивановский. // Труды ЦНИИС, вып. №202. — М.: ЦНИИС, 2000.
- Пановко Я.Г. Динамический расчет сооружений //Строительная механика в СССР 1917-1957 гг. М: 1957 — С. 178.
- Пановко Я.Г. Устойчивость и колебания упругих систем / Пановко Я.Г., Губанова И.И. / М.: — 1967. — С. 162.
- Пановко Я.Г. Основы прикладной теории колебаний и удара. М: Машиностроение. — 1976. — С. 321.
- Пановко Я.Г. Введение в теорию механического удара. М.: Наука 1977. — С. 224.
- Паримбетов А.А. Экспериментальные исследования воздействия малых масс на металлическую балку железнодорожного моста / Паримбетов А.А., Бондарь И.С. // Сборник научных трудов профессорско-преподавательского состава и студентов посвященной 135-летию М. Тынышпаева «Транспорт в XXI веке: состояние и перспективы» — Алматы, 2016. — С. 610-614.
- Пейн Г. Физика колебаний волн. М: Мир. — 1979. — С. 389.
- Поляков В.Ю. Взаимодействие подвижного состава с элементами мостового перехода при высокоскоростном движении. Диссертация на соискание ученой степени доктора технических наук. Москва 1994 — 395 с.
- Сато Юкио. Обработка сигналов / под редакцией Ёсифуми Амэмия. 1999. — С. 175.
- Сергеев A.A. Методы учета динамических воздействий подвижной нагрузки на пролетные строения мостов / Сергеев A.A., Андронов A.A. // Научные труды ОАО ЦНИИС. — М: 2006 — Вып. 230. — С. 21-25.
- Сергиенко А.Б. Цифровая обработка сигналов. СПб. Издательство: Литер, 2002. — С. 608.
- Снитко Н.К. Методы расчета сооружений на вибрацию и удар.-Л.: Стройиздат, 1953 — С. 288.
- Снитко Н.К. Динамика сооружений — М: Госстройиздат, 1960. — С. 310.
- Стрелецкий Н.С. О природе динамического коэффициента и дополнительных напряжений. Избранные труды. М.:Стройиздат,1975 — С. 112.
