Сравнительный анализ динамических качеств грузовых вагонов с разными типами тележек

Оглавление

Цикл статей:

Глава 1 — Совершенствование технологии эксплуатации грузовых вагонов с инновационными тележками
Глава 2 — Сравнительный анализ динамических качеств грузовых вагонов с разными типами тележек
Глава 3 — Исследование динамической нагруженности грузовых вагонов с нелинейным рессорным подвешиванием ходовой части в системе «вагон-путь»
Глава 4 — Технология эксплуатации грузовых вагонов с инновационными тележками по гарантийным участкам повышенной протяженности

Формирование расчетной схемы и математической модели механической системы «вагон-путь»

Силовые характеристики рессорных комплектов тележек 18-100, 18-9855 и 18-194-1

Комплект пружин центрального рессорного подвешивания тележки 18-100 грузовых вагонов с осевой нагрузкой 23,5 тс состоит из семи пар сдвоенных (внутренней и наружной) винтовых пружин равной высоты и статическими прогибами: в порожнем состоянии вагона — 8 мм; в груженом — 48 мм [1; 18; 19; 22; 72].
Конструктивное исполнение рессорного комплекта тележек Barber (модели 18-9810 и 18-9855) отличается от тележек 18-100. Это отличие, кроме количества двойных пружин, заключается в том, что в тележке Barber нагружение пружин происходит последовательно: сначала упруго деформируются подклиновые внутренние, затем — подклиновые наружные, после этого — внутренние под надрессорной балкой и наконец — наружные под надрессорной балкой. Вследствие этого силовая характеристика, построенная в результате проведенных экспериментальных измерений при участии автора в вагонном ремонтном депо Московка АО «Вагонная ремонтная компания-2», является кусочно-линейной (представлено на рисунке 2.1, сплошная линия), состоящей из четырех участков: 1-й участок — работа подклиновых внутренних пружин, 2-й участок — работа подклиновых наружных и внутренних пружин, 3-й участок — в дополнение к предыдущим пружинам подключаются внутренние пружины под надрессорной балкой, 4-й участок — работа всех пружин рессорного комплекта. На этих же характеристиках указаны рабочие точки для порожнего и груженого режимов работы вагона на тележках 18-100 и 18-9855 при статической нагрузке в
порожнем и груженом состояниях. Для сравнения на этом же рисунке представлена аналогичная характеристика рессорного комплекта для тележки 18-100 (рисунок 2.1, штриховая линия).

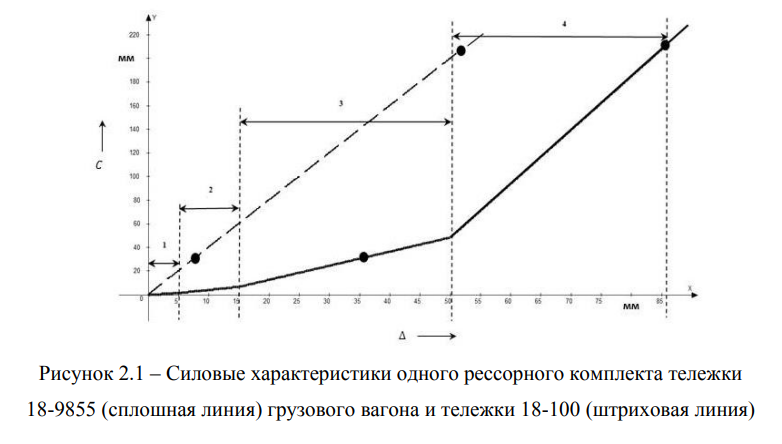
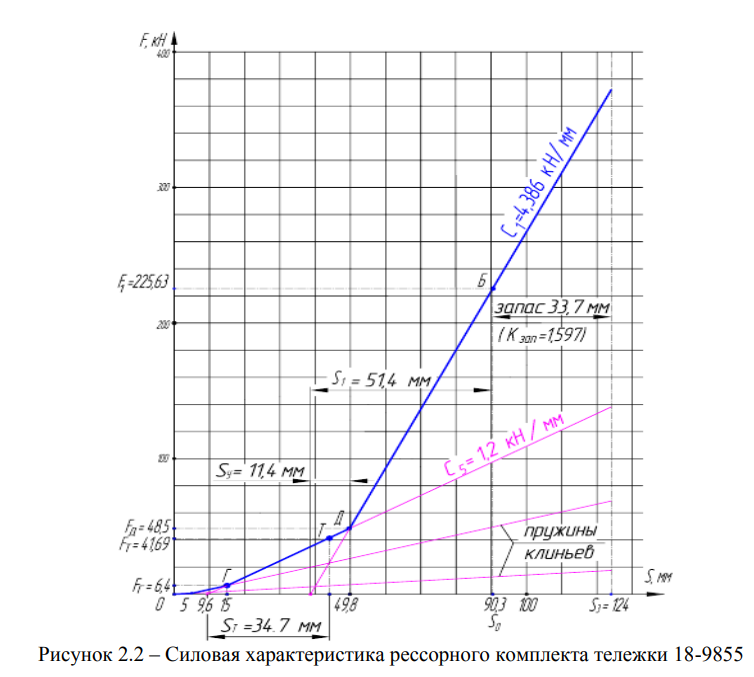
Для вагона с тележкой 18-9810 величина статического прогиба в порожнем состоянии составляет Д= 34 мм и 86 мм — под нагрузкой брутто. Для вагона с тележкой 18-100 эти же деформации составляют: Д = 8 мм — для порожнего, для груженого — 48 мм. Построенные характеристики практически совпадают с характеристиками, приведенными в работе [55] (рисунок 2.2).

В той же работе [55] приведена силовая характеристика рессорного комплекта тележки 18-194-1 вагонов, выпускаемых ОАО «НПК Уралвагонзавод» (рисунок 2.3).

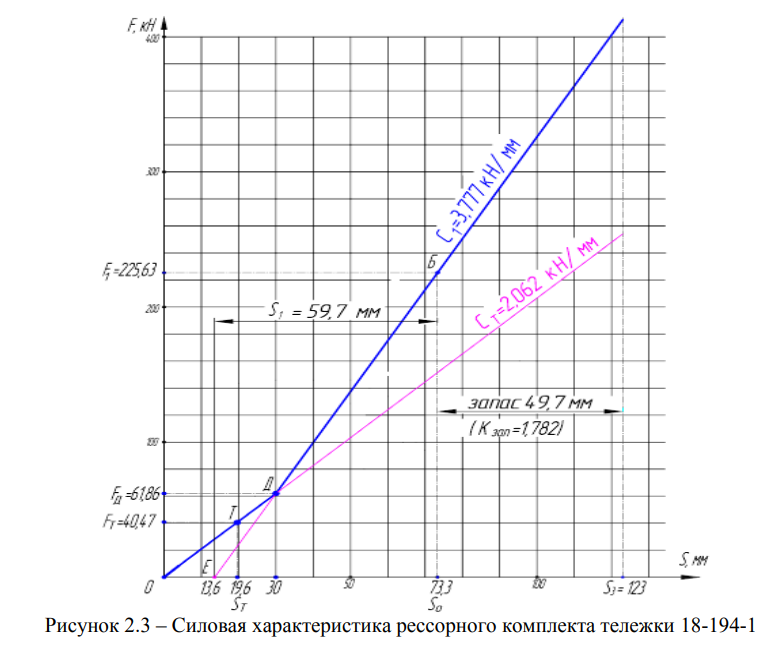
Очевидно, что в порожнем состоянии вагонов статический прогиб рессорного комплекта тележки 18-100 (вагон модели 12-132) составляет всего 8 мм, а у тележки 18-9855 больше, чем у тележки 18-194-1, что обеспечивает вагону модели 12-9853, выпускаемому ЗАО «Тихвинский ВСЗ», лучшие динамические качества в этом режиме движения по сравнению с вагоном модели 12-132 (нагрузка на ось 23,5 тс) и вагоном 12-196-01, выпускаемым ОАО «НПК «Уралвагонзавод». Вместе с тем под нагрузкой брутто жесткость рессорного комплекта тележки 18-9855 в 1,16 раза больше, чем у тележки 18-194-1, и в 1,12 раза больше, чем жесткость рессорного комплекта тележки 18-100. При этом собственная частота колебаний подпрыгивания вагона с тележкой 18-194-1 на 7,7 % ниже по сравнению с вагоном на тележках модели 18-9855, что благоприятно с точки зрения повышения плавности хода вагона и сохранности грузов. Конструктивный запас прогиба рессорного комплекта тележки 18-194-1 составляет 49,6 мм, а у тележки 18-9855 — только 33,7 мм. Малое значение конструктивного запаса может привести к полному смыканию витков пружин рессорного комплекта при движении вагона по пути с большими неровностями в случае возникновения резонансного режима колебаний, а также в совокупности с большой боковой ветровой нагрузкой, приводящей к валкости кузова.

Возмущения, действующие на механическую колебательную систему «вагон-путь»

Оценке состояния пути и его влиянию на подвижной состав посвящено достаточно большое количество теоретических и прикладных исследований и изобретений [6; 8-14; 24; 26; 35-36; 61; 73; 76-78; 84-85; 87; 97-104], в том числе авторов П.С. Анисимов, М.Ф. Вериго, Л.О. Грачевой, Ю.П. Бороненко, Г.И. Петрова, А.М. Орловой, В.Д. Хусидова, П.С. Анисимова, А.В. Смолянинова, В.Ф. Лапшина, А.Э. Павлюкова, Е.А. Рудаковой, А.Я. Когана, C.B. Вершинского, В.Н. Данилова, И.И. Челнокова, И.И. Галиева, В.А. Нехаева, В.А. Николаева, В.К. Гарга, Р.В. Дуккипати, А.М. Годыцкий-Цвирко, A.A. Львова, В.П. Ефимова,

А. Пранова, В.А. Лазаряна, В.А. Каблукова, О.М. Савчука, М.А. Левинзона,
В. Лукина, Ф.П. Федосеева, Ю.С. Ромена, В.Ф. Ушкалова, JI.M. Резникова,
Ф. Редько и др.

Возмущения, действующие на железнодорожный экипаж, можно разделить на три вида: кинематические, силовые и параметрические.

Применительно к условиям работы магистрального подвижного состава в качестве кинематических возмущений выступают геометрические неровности пути в профиле и в плане, неровности на поверхности катания колес. В качестве силовых возмущений могут выступать периодические силы, обусловленные дисбалансом колесных пар. Параметрические возмущения обусловлены изменением какого-либо параметра системы, например, разностью жесткости пути по длине под шпалой и в пролете между шпалами, а также в зоне стыка.

Однако, как показано в работе [5], результаты многочисленных исследований взаимодействия подвижного состава и пути не обнаруживают явлений, свойственных параметрическим колебаниям подвижного состава при движении со скоростями, установленными для грузовых поездов.

В качестве входных возмущающих воздействий при проведении расчетов необходимо использовать корректные модели неровностей железнодорожного пути, которые, вообще говоря, являются случайными, но в отдельных случаях для выявления резонансных явлений и пр. их часто применяют в детерминированной форме записи [5; 37; 21; 40; 74; 29; 82].

Оптимизация параметров ходовых частей железнодорожного подвижного состава показывает [56], что в исследованиях динамических свойств подвижного состава применяют в основном две модели пути: дискретную, по которой характеристики пути учитываются в виде приведенных к колесу сосредоточенных масс, упругости и демпфирования; и континуальную, в которой путь моделируется балкой на сплошном упругом основании с распределенными массой и силой трения. Верхнее строение пути рассчитывают как балку бесконечной длины на сплошном упругом основании [67], поэтому и в динамических расчетах показателей качества экипажных частей вагонов при учете пути в виде континуальной модели представляется возможным выявить важные особенности колебательного процесса системы «колесо-рельс» по сравнению с дискретной моделью. Для амплитудно-частотных характеристик (далее — АЧХ) кузова результаты расчетов при дискретной и континуальной моделях пути практически совпадают (расхождение не превышает 10-12 %) [82], поэтому при расчете колебаний узлов грузового вагона и пути вполне допустимо использовать обычную дискретную модель пути.

Природа этих возмущений носит как геометрический, так и динамический характер. К первому из них относятся неровности рельсового пути (волнообразный износ поверхностей катания рельсов, пробоксовины, выщербины и зазоры в стыках рельсов и др.), а также несовершенства поверхностей катания колес (ползуны, выщербины, навар, неравномерный прокат). Динамическое воздействие на подвижной состав определяется неравножесткостью верхнего строения пути в сечениях между шпалами и под шпалами, а также в зоне стыка рельсов, состоянием балластного слоя, возможными зазорами между элементами путевой структуры (рельсами, подкладками и шпалами).

На основании проведенных теоретических и экспериментальных исследований ВНИИЖТ разработал Руководящий документ [73], содержащий выражения расчетных неровностей пути во временной и частотной областях, которые и будут использованы при исследованиях. Применяемые в качестве возмущения эквивалентные расчетные неровности представляют собой обобщенную характеристику возмущения, в которую входят как геометрические неровности рельса, неровности кругов катания, так и неравномерность характеристик пути по его длине, поэтому они и будут использованы в дальнейшем.

Применяемый теоретический метод исследования колебаний грузовых вагонов позволяет учитывать все наиболее характерные конструктивные особенности ходовых частей и даже на стадии проектирования экипажа [39; 63], показано, например, в работе [80], как выявить влияние различных параметров экипажа на устойчивость его движения и на другие его динамические качества.

Для оценки влияния значений конструктивных параметров ходовой части грузового вагона на его динамическую нагруженность, обусловленную движением по неровностям пути, целесообразно ограничиться исследованием вертикальных колебаний экипажа, поскольку, как отмечено в работе [66], «проанализировать полученные результаты при численном интегрировании сложной пространственной модели колебаний такой системы трудно из-за взаимного влияния колебаний с различными частотами и фазами».

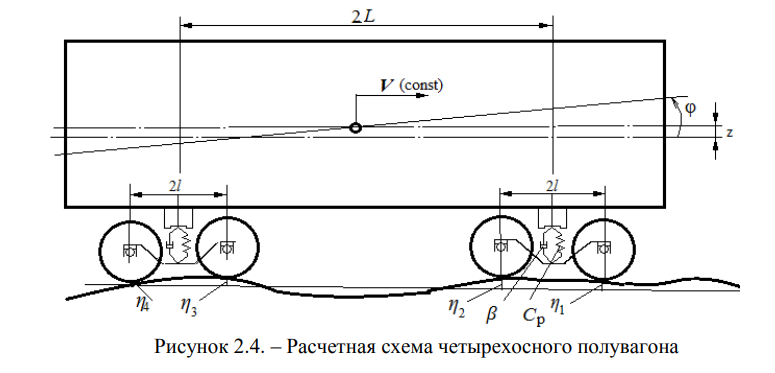
Составим расчетную схему механической колебательной системы «вагон- путь» в вертикальной продольной плоскости симметрии экипажа (см. рисунок 2.1 ), на которой отмечены ее инерционные, жесткостные и диссипативные параметры, а также обобщенные координаты, описывающие движение отдельных узлов этой системы. Будем полагать железнодорожный экипаж симметричным, а колебания — малыми. Заменим сухое трение, создаваемое клиновыми фрикционными гасителями колебаний, эквивалентным вязким, согласно методу, предложенному С.П. Тимошенко [38].

Предварительные допущения, принятые при формировании расчетной модели механической системы «вагон-путь»

Совершенствование конструкций ходовой части грузовых вагонов за счет улучшения рессорного подвешивания диктует острую необходимость выполнения сравнительной оценки эффективности динамических качеств нового подвижного состава.

Для получения оценок динамических свойств механической колебательной системы «вагон-путь» необходимо:

создание расчетной схемы, отображающей основные динамические свойства исследуемой модели;
выбор возмущающего воздействия на вход этой системы;
формирование методами аналитической механики математической модели процессов, возникающих при движении грузового вагона, и ее исследование.

Будем полагать, что кузов и все узлы тележки (надрессорные балки, боковые рамы и колесные пары) являются абсолютно твердыми телами. Массу надрессорных балок трехэлементных тележек отнесем к массе кузова, так как рассматриваются только вертикальные колебания данной системы. Будем также считать, что перевалка кузова на подпятниках отсутствует.

Результаты этого исследования аналитическими методами (для моделей с малым числом степеней свободы) и методами эквивалентного преобразования [86], а также методами численного интегрирования с применением пакета прикладных программ MathCad позволяют дать сравнительную оценку влияния конструкции рессорного подвешивания ходовой части вагонов на показатели их динамических качеств при движении с различными скоростями.

Показатели динамических качеств подвижного состава (плавность хода, влияющая на сохранность перевозимых грузов, динамические силы в рессорном подвешивании и др.), зависят от параметров рессорного подвешивания его ходовой части и от уровня возмущений, действующих со стороны пути на подвижной состав [65].

Математическая модель и анализ вынужденных колебаний вагона при движении с геометрической неровностью

Для формирования математической модели воспользуемся энергетическим алгоритмом Лагранжа [34]. Для сравнения динамических свойств вагонов на разных тележках рассмотрим движение их по рельсовому пути с геометрическими неровностями, значения параметров которых приняты в соответствии с Руководящим документом ВНИИЖТ [73] с разными скоростями при одинаковых параметрах неровностей (амплитудой и длиной Ь_н). Расчетная схема вагона приведена на рисунке 2.4, где 2 и ^ — обобщенные координаты подпрыгивания и галопирования кузова вагона.

Принимая упрощения и допущения, обычно используемые в курсе «Динамика подвижного состава железных дорог», рассмотрим плоское движение четырехосного полувагона. Сначала примем железнодорожный путь абсолютно жестким, тогда для составляемой математической модели, описывающей колебания подпрыгивания и галопирования кузова, геометрические неровности поверхности катания рельсов т](х), где х — пройденное вагоном расстояние с момента начала движения. Считая скорость движения постоянной величиной, получим, что х равно:

Кинетическая энергия кузова вагона:

Форма записи (2.3) здесь использована потому, что в дальнейших исследованиях силовая характеристика рессорного подвешивания будет нелинейной функцией прогиба. В первоначальном варианте усилие в рессорном комплекте является линейной функцией его деформации, т.е.:

С учетом выражений (2.6), (2.7) и (2.8) вместо формулы (2.5) имеем:

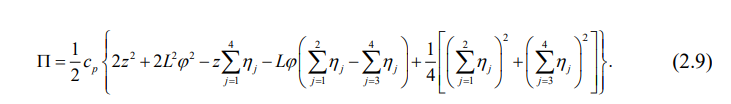
В виду того, что для вывода математической модели поведения вагона будет использован энергетический метод уравнений Лагранжа второго рода, который предполагает взятие частных производных от потенциальной энергии кузова (2.9) по обобщенным координатам [60]: 2 — подпрыгивание кузова вагона, отсчитываемое от положения его статического равновесия; ф — галопирование кузова вагона, также отсчитываемое от положения его статического равновесия (положительное при повороте против часовой стрелки), то в выражении (2.9) можно отбросить слагаемое, заключенное в квадратные скобки. Тогда в окончательном виде потенциальная энергия кузова вагона запишется так:

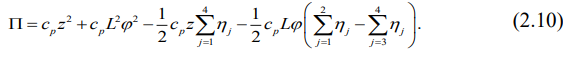
Вычислим диссипативную функцию рессорного подвешивания, заменив сухое трение эквивалентным вязким в зависимости от того, какой вид внешнего возмущения будет принят в дальнейшем:

С учетом зависимостей (2.7) и (2.8) имеем:

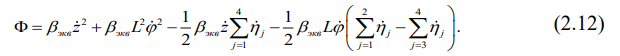
Очевидно, что при движении вагона по жесткому железнодорожному пути, нужно составить всего два дифференциальных уравнения относительно подпрыгивания и галопирования кузова вагона, которые запишем сначала в виде дифференциальных уравнений Лагранжа второго рода:

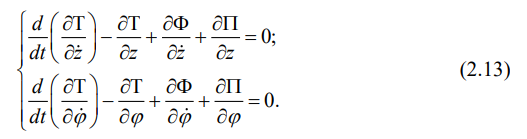
Взяв соответствующие производные, имеем:

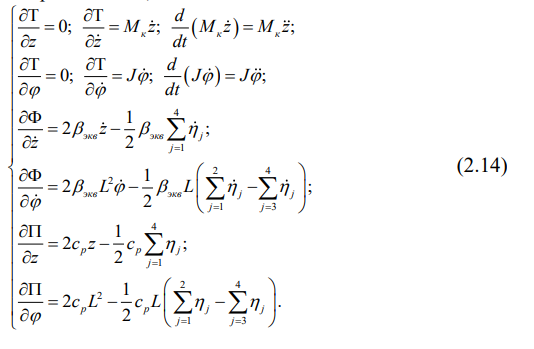
Их подстановка в систему (2.13) дает математическую модель колебаний кузова вагона при движении по жесткому железнодорожному пути:

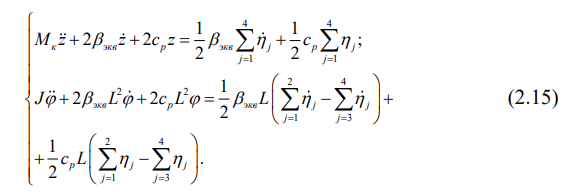
Итак, динамическое поведение кузова вагона, обладающего вертикальной осью симметрии, описывается двумя обыкновенными, линейными дифференциальными уравнениями второго порядка. Причем каждое уравнение может исследоваться отдельно от другого уравнения. Разделив первое уравнение системы (2.15) на массу кузова, перепишем его в виде:

Разделив второе уравнение системы (2.15) на момент инерции кузова, получим обыкновенное, линейное дифференциальное уравнение вида:

Дифференциальные уравнения (2.16) и (2.17) могут быть достаточно легко проинтегрированы, так как они линейные и обладают разработанным высшей математикой регулярным методом их решения, однако, прежде всего, обратим внимание на запаздывание воздействия на соответствующих колесных парах. Время запаздывания возмущения дано в таблице 2.1.

Следовательно, нетрудно написать такие формулы, характеризующие поступление внешнего возмущения, в механическую систему:

Тогда вместо уравнения (2.16) получим:

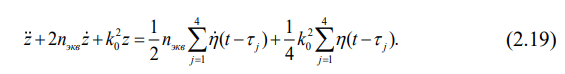
Уравнение (2.17) приводится к виду:

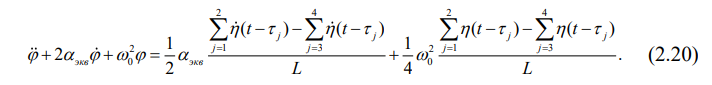
Итак, для мониторинга динамического состояния вагонов на тележках 18-100 имеется практически все, кроме вида внешнего возмущения, действующего со стороны пути. Это возмущение будем выбирать в соответствии с Руководящим документом ВНИИЖТ.

Динамические качества вагона, как и любого железнодорожного экипажа,
оцениваются соответствующими показателями динамических качеств,
коэффициентами динамики, ускорениями различных узлов подвижного состава,
динамическими силами в рессорном подвешивании, а также воздействием на железнодорожный путь.

Найдем для нашей расчетной схемы давление колесных пар на путь, учитывая, что колесные пары не отрываются от рельсов, а сам железнодорожный путь абсолютно жесткий. Расчетная схема показана ниже на рисунке 2.5.

Запишем уравнения движения этой простой механической системы, но сначала определим углы поворота тележек вагона:

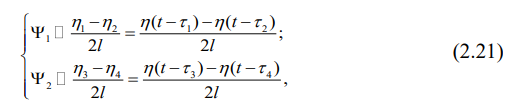
а затем вычислим вторые производные по времени от этих углов, получая угловые ускорения:

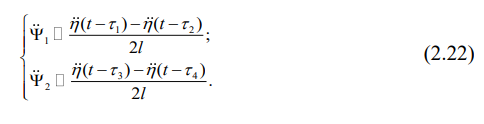
В результате имеем следующую систему уравнений:

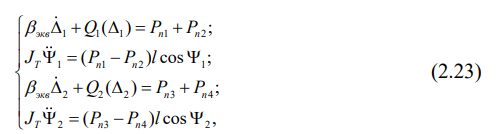
где JT – момент инерции тележки относительно ее центра масс.

Подставляя в (2.23) выражения (2.21) и (2.22), разрешим с помощью формул Крамера систему уравнений относительно давлений колесных пар на железнодорожный путь:

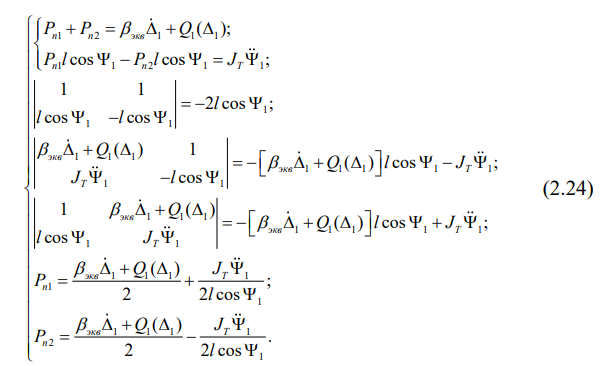
Последние два выражения в системе (2.24) и дают формулы для вычисления давления на железнодорожный путь первой и второй колесных пар:

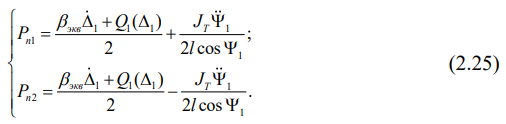
Применяя метод математической индукции, напишем формулы, по которым рассчитываются давления на путь для третьей и четвертой колесных пар:

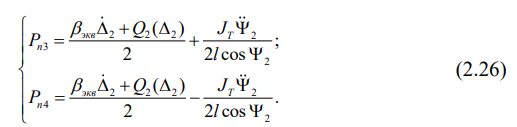
Обратим внимание на тот факт, что не учет момента инерции тележки вагона приводит к тому, что давления первой и второй колесных пар становятся равными друг другу. Также одинаковыми будут в этом случае давления третьей и четвертой колесных пар.

Результаты численного интегрирования дифференциальных уравнений движения вагона на тележках 18-100 в порожнем и груженом режимах его движения приведены на рисунках 2.6 — 2.9.

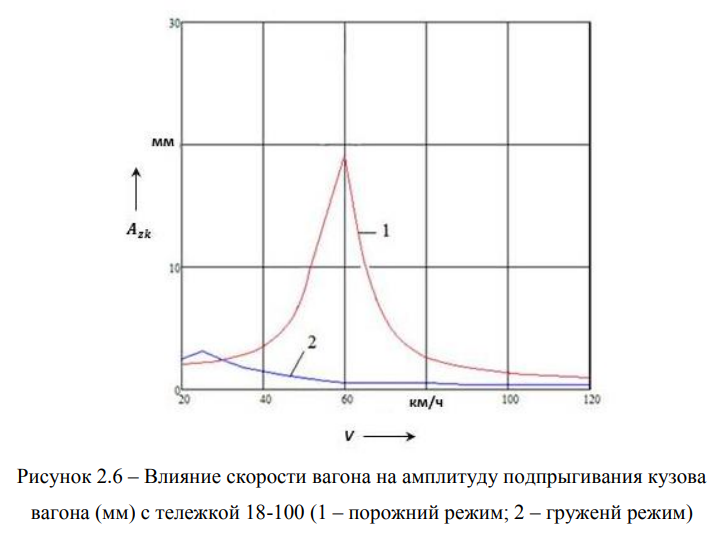
Из графика, приведенного на рисунке 2.6, видно, что при движении порожнего вагона на скорости 60 км/ч происходит резонансный режим вертикальных колебаний кузова, что негативно влияет на условия контакта колеса такого вагона с рельсом.

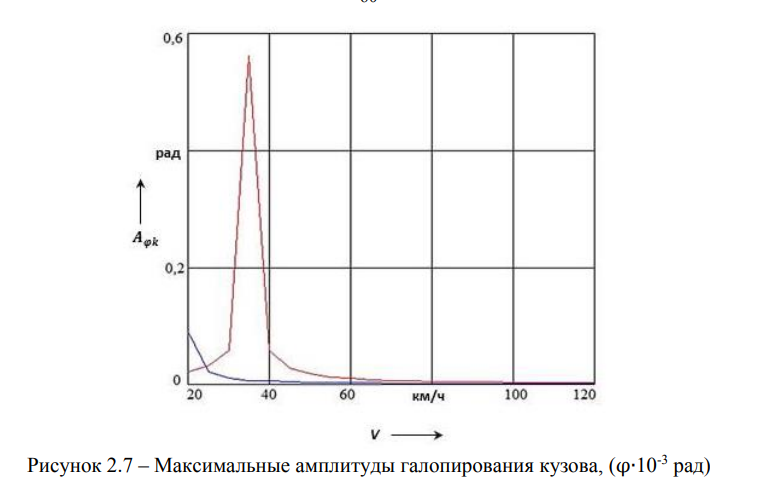
Резонансная скорость движения груженого вагона приходится на режим разгона и равна 26 км/ч. Этот фактор благоприятно сказывается на динамическом поведении груженого вагона, поскольку его движение с установленной скоростью поезда происходит в зарезонансном режиме вертикальных колебаний. Максимальные амплитуды галопирования кузова приходятся на диапазон скорости 35 км/ч (рисунок 2.7).

Зависимость максимальных ускорений подпрыгивания кузова порожнего от
скорости движения поезда приведена на рисунке 2.8.

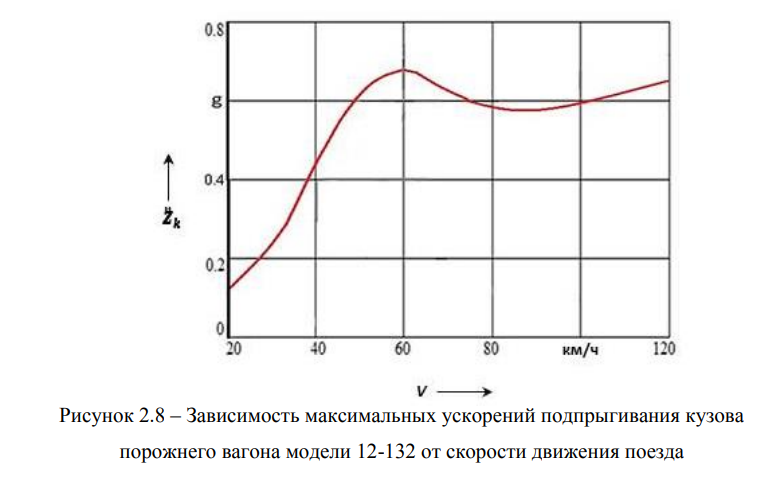
Зависимость максимальных ускорений подпрыгивания кузова порожнего
вагона модели 12-132 с тележкой 18-100 от скорости движения поезда приведена
на рисунке 2.9.

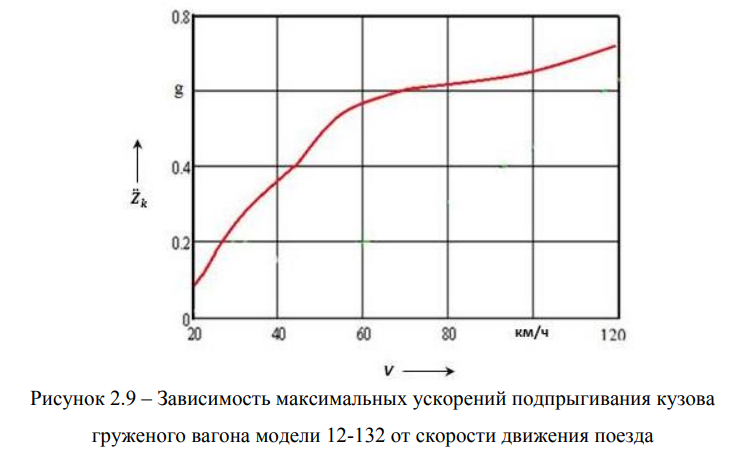
Анализ графиков, приведенных на рисунках 2.8 и 2.9, показывает, что
показатели динамических качеств этих вагонов не отвечают современным
требованиям с точки зрения обеспечения безопасности движения поезда в
порожнем режиме. Так из рисунка 2.8 видно, что вертикальные ускорения кузова
порожнего вагона достигают значительных величин, что приводит к колебаниям
сил взаимодействия в системе «колесо-рельс».

Сравнительный анализ динамических свойств вагонов при их движении по упругому пути

Вновь обратимся к вагону на стандартных тележках 18–100, но теперь
железнодорожный путь представлен дискретной инерционно-диссипативной
математической моделью. Опытом и теоретическими исследованиями
установлено, что в диапазоне частот от 0 – 30 Гц амплитуды гармонических составляющих амплитудно-частотной характеристики (далее – АЧХ) буксового
узла отличаются от амплитуд возмущений не более чем на 13%. Более того, АЧХ
железнодорожного пути представляет собой одногорбую кривую, обычно
характерную для одноступенных механических моделей. На колебания колес
практически не влияют колебания надрессорного строения экипажа. Если
варьировать параметры рессорного подвешивания, уменьшая или увеличивая их в
10 раз, то АЧХ буксового узла изменяются не более чем на 10 – 12%. При выборе
расчетной схемы объединенной механической системы «экипаж-путь» примем во
внимание, что целью данного исследования является анализ динамических
процессов, протекающих в элементах экипажа, то, что происходит при этом в
элементах пути, в рамках данной работы не рассматривается. В связи с этим
необходимо выбрать достаточно подробную схему экипажа, что дает право
ограничиться учетом лишь приближенных интегральных характеристик пути
(рисунок 2.10).

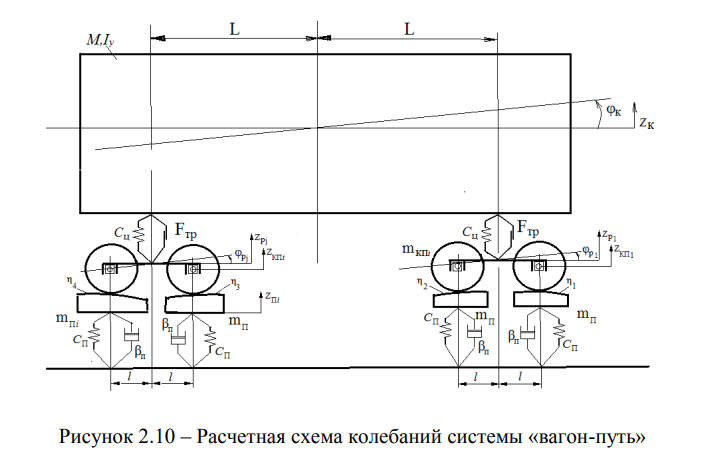
Таким образом, необходимо дополнить кинетическую энергию экипажа
(2.2), движущегося безотрывно по рельсам железнодорожного пути, кинетической энергией колесных пар, которые теперь совершают колебания подпрыгивания.
Итак, имеем:

Подставляя (2.29) в (2.27) и отбрасывая квадраты геометрических неровностей, получим в окончательном виде выражение для кинетической энергии вагона, движущегося по инерционному упругому железнодорожному пути:

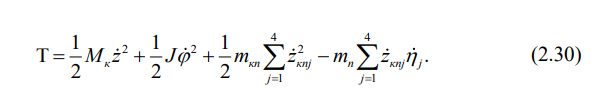
Нуждается в корректировке и потенциальная энергия механической системы «экипаж-путь», так как железнодорожный путь обладает упругостью, которая способна запасать потенциальную энергию. Итак, вместо (2.7) имеем:

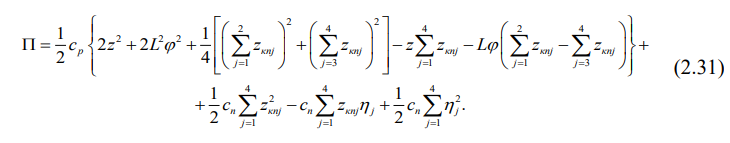
В виду того, что потенциальная энергия всегда вычисляется с точностью до некоторой постоянной, то последним слагаемым в (2.31) можно пренебречь, тем более потому, что частные производные от потенциальной энергии берутся только по обобщенным координатам, а геометрическая неровность железнодорожного пути n в них не входит. Окончательно напишем:

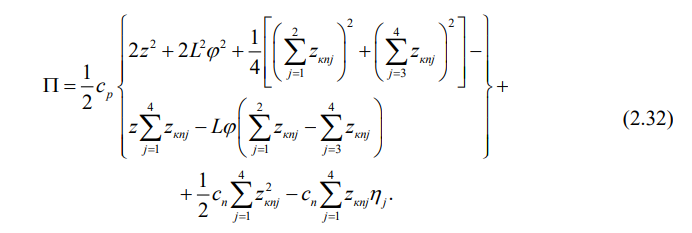
Раз уж учтен железнодорожный путь в виде дискретной инерционно-диссипативной математической модели, то возникает потребность и в
корректировке диссипативной функции механической системы «экипаж-путь»
(2.12), ибо последний тоже рассеивает энергию колебаний. Сравнение выражений
(2.10) и (2.12) указывает на то, что следует воспользоваться методом
математической индукции, в результате получим:

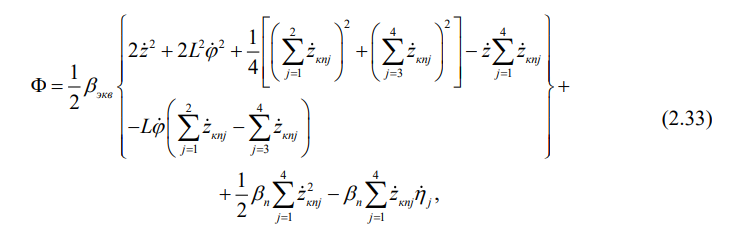
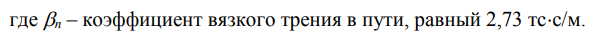
Уравнения Лагранжа второго рода вновь дают возможность составить
математическую модель колебаний вагона на тележках 18-100 при его движении
по железнодорожному пути с неровностями на поверхности катания рельсов:

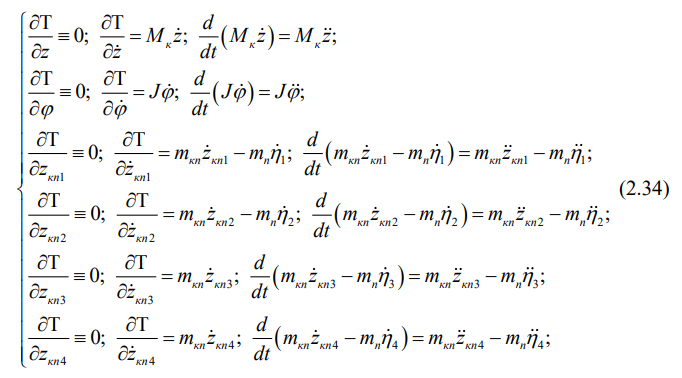
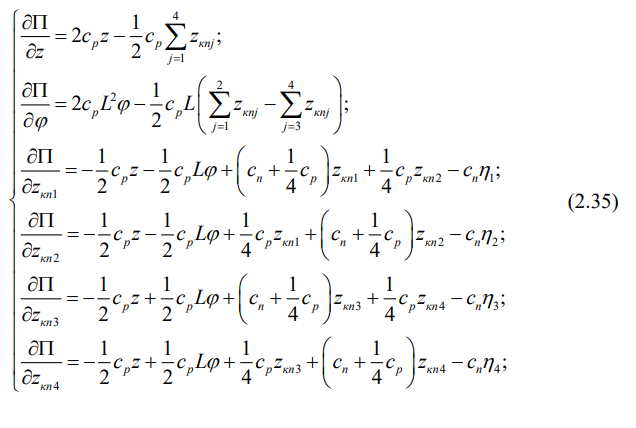
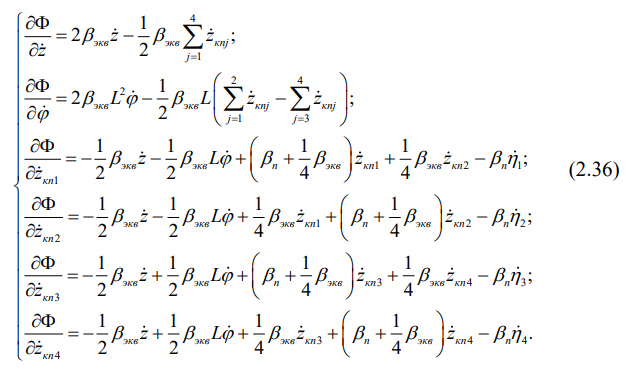
Обыкновенные дифференциальные уравнения колебаний подпрыгивания и галопирования кузова вагона на тележках 18-100 и подпрыгивания его колесных пар представляются следующей системой:

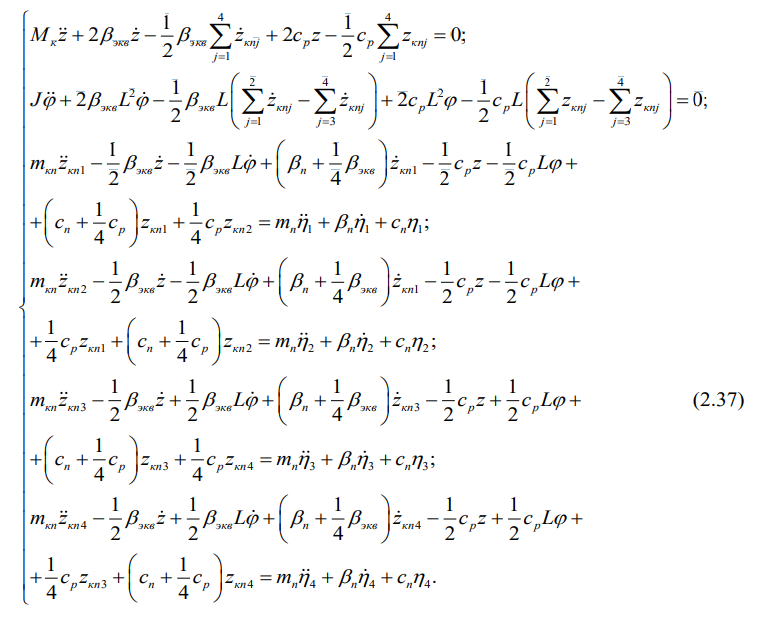
Если ранее при изучении движения вагона на тележках 18-100 по абсолютно жесткому железнодорожному пути его геометрические неровности непосредственно влияли на формирование сил в контакте колес и рельсов и на динамику узлов вагона, то учет упругости пути приводит к тому, что внешние возмущения в рассматриваемом случае зависят от характера взаимодействия колесных пар с верхним строением упругого пути. Воздействие на кузов теперь будет зависеть от отмеченного фактора. Заметим еще, что ранее уравнения подпрыгивания и галопирования кузова исследовались отдельно друг от друга вследствие симметрии экипажа, т.е. приходилось иметь дело с одноступенными математическими моделями. В данном случае математическая модель динамики вагона обладает шестью степенями свободы, а это существенным образом усложняет аналитическое исследования динамического поведения вагона.

Получим математическую модель колебания вагона на тележках Barber при движении по упруго-диссипативному железнодорожному пути, который вновь представим дискретной инерционно-диссипативной моделью.

Принципиальное отличие вагона на тележках 18-100 от вагона на тележках Barber состоит в том, что для последнего, как показывает экспериментальное исследование, рессорное подвешивание имеет нелинейную силовую характеристику, показанную на рисунке 2.1, где сила в кН, а прогиб в м.

Кинетическая энергия для этого случая уже нами получена ранее (2.27).

Изменится лишь выражение потенциальной энергии:

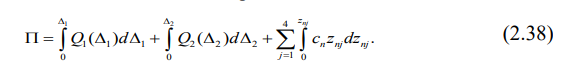
Исходная потенциальная энергия дополнена потенциальной энергией, которую запасает железнодорожный путь. Напомним, что силовая характеристика вагона на тележках Barber, согласно выражениям (2.1), нелинейна и описывается полиномом:

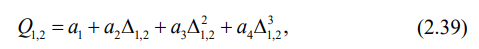
где прогибы рессорного подвешивания равны:

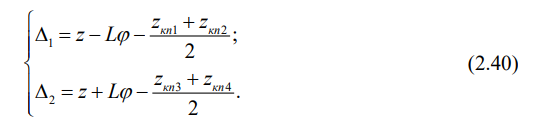
В дальнейшем понадобятся частные производные от прогибов рессорного подвешивания вагона по обобщенным координатам. Определим их:

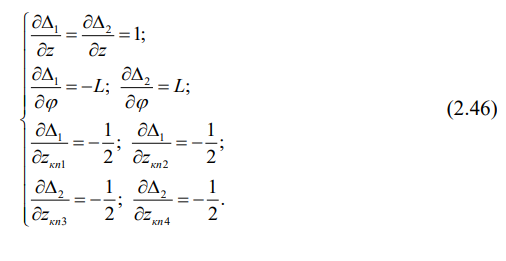
Взяв необходимые производные от кинетической и потенциальной энергий и диссипативной функции и подставив эти результаты с учетом выражений (2.46) в систему (2.47), получим систему обыкновенных нелинейных дифференциальных уравнений шестого порядка:

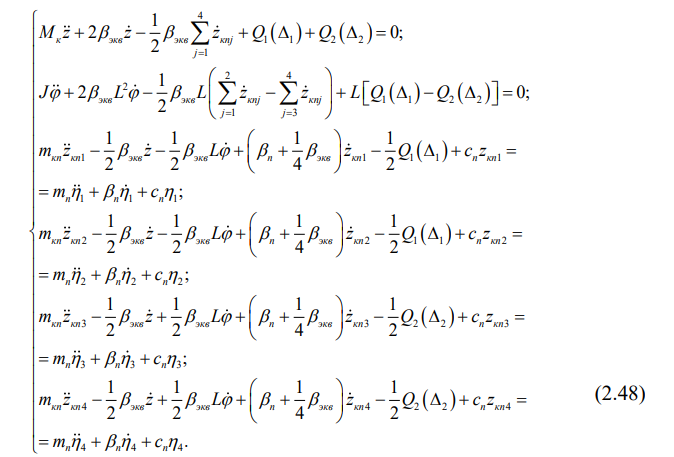
Итак, геометрические неровности на поверхности катания рельсов железнодорожного пути оказывают воздействие только на колесные пары вагона.

Выведем формулы, позволяющие оценить воздействие вагона на железнодорожный путь:

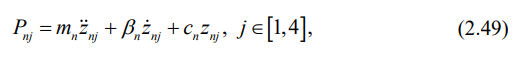
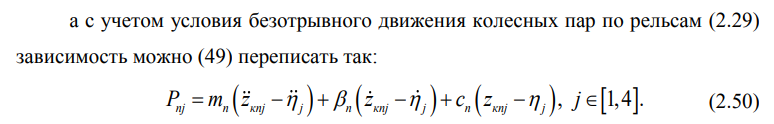
Зависимость амплитуды подпрыгивания кузова порожнего вагона с тележкой 18-9855 от скорости представлена на рисунке 2.11.

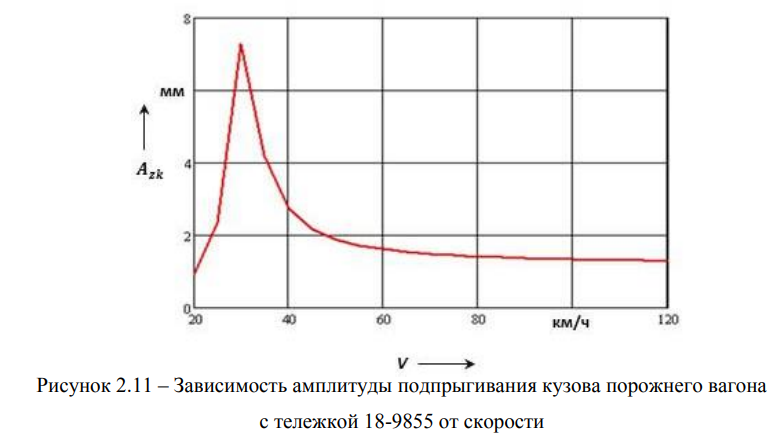
Из графика, представленного на рисунке 2.11, видно, что по сравнению с вагоном, оснащенным типовой тележкой 18-100, вагон модели 12-9853 с тележкой 18-9855 обладает лучшими динамическими качествами. Так, в порожнем режиме движения его резонансная скорость равна 30 км/ч и приходится на режим разгона поезда, в то время как критическая скорость вагона модели 12-132 с типовой тележкой 18-100 равна 58 км/ч, т.е. приходится на диапазон установленной скорости движения порожнякового поезда.

Зависимость амплитуды подпрыгивания кузова груженого вагона с тележкой 18-9855 от скорости его движения приведена на рисунке 2.12.

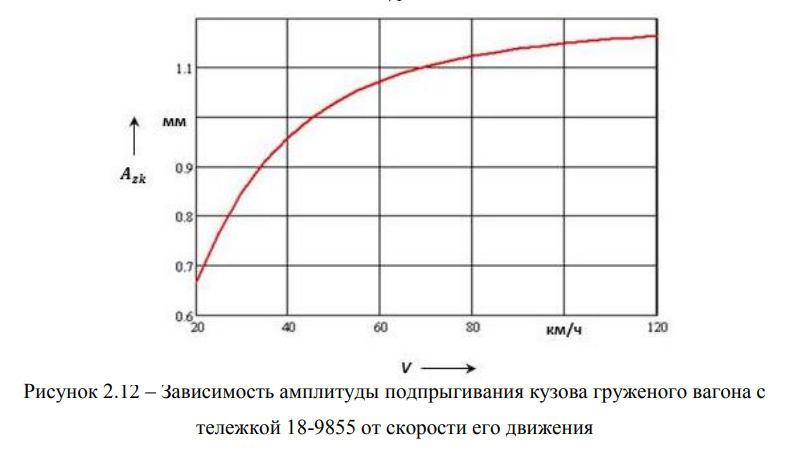
Из графика видно, что в зоне ходовых скоростей движения поезда в груженом режиме его движения по равноупругому пути амплитуда подпрыгивания весьма мала и составляет 1,0 -1,15 мм.

Влияние скорости движения на амплитуду ускорений подпрыгивания порожнего вагона показано на рисунке 2.13.

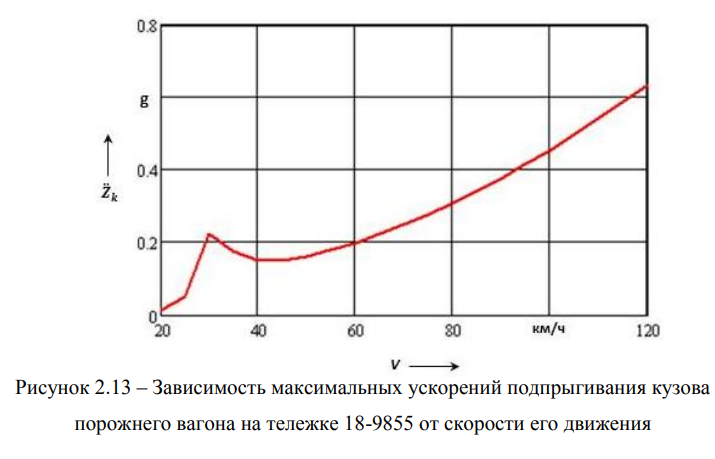
Из графика, приведенного на рисунке 2.13, видно, что резонансная скорость вагона с тележкой Barber приходится на стадию разгона поезда, в то время как порожний вагон с тележкой 18-100 на скорости 60 км/ч движется в резонансном режиме, что негативно влияет на безопасность движения поезда.

Кроме того, в таком режиме имеет место интенсивный износ контактируемых между собой поверхностей фрикционного клина, наклонной поверхности кармана боковой рамы и вертикальной поверхности фрикционной планки.

Влияние скорости движения груженого вагона на тележке 18-9855 на максимальные ускорения подпрыгивания его кузова представлено на рисунке 2.14.

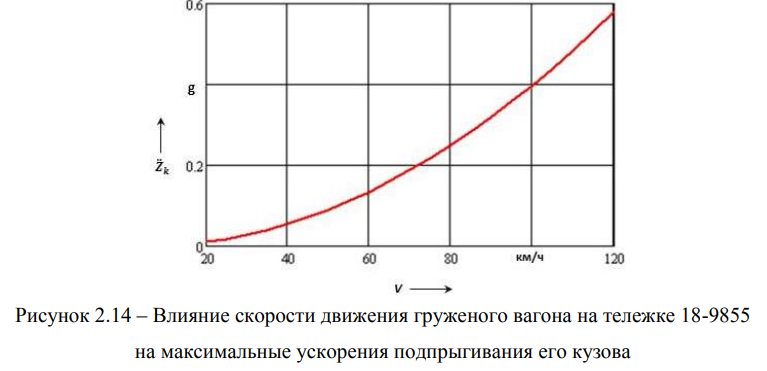
Из графика, приведенного на рисунке 2.14. видно, что с ростом скорости увеличиваются и ускорения кузова, которые при скорости 100 км/ч достигают 0,4 что можно объяснить большей, по сравнению с тележкой 18-100, жесткостью рессорного комплекта с соответствующим увеличением сил трения из-за увеличения угла наклона фрикционного клина (55° у тележки 18-9855 и 45° у тележки 18-100).

Список литературы

Захаров, С.М. Математическое моделирование влияния параметров пути и подвижного состава на процессы изнашивания колеса и рельса / С.М Захаров, Ю.С. Ромен // Вестник ВНИИЖТ. — 2010. — № 2. — С. 26-30.
Ильин, И.П. Особенности экономического анализа эксплуатационных расходов на пассажирские перевозки / И.П. Ильин // Экономика железных дорог. — 2015. — № 1. — С. 71-84.
Инструкция по техническому обслуживанию вагонов в эксплуатации [Электронный ресурс] // Совет по железнодорожному транспорту государств-участников Содружества. — 2009. — 154 с. — Режим доступа: https://www.ldz.lv/sites/default/files/08 PV Padome 50 Piel.%2017 2.pdf.
Камаев, В.А. Оптимизация параметров ходовых частей железнодорожного подвижного состава / В.А. Камаев. — М.: Машиностроение, 1980. — 215 с.
Классификатор «Основные неисправности грузовых вагонов» (К ЖА 2005 04): утвержден Комиссией Совета по железнодорожному транспорту полномочных специалистов вагонного хозяйства железнодорожных администраций (Протокол заседания от 23-25 марта 2004 г.).
Кобаская, И.А. Технология ремонта подвижного состава: Учебное пособие / И.А. Кобаская. — М.: УМЦ ЖДТ, 2016. — 288 с.
Кобзарь, А.И. Прикладная математическая статистика. Для инженеров и научных работников / А. И. Кобзарь. — М.: Физматлит, 2006. — 816 с.
Конышев, С.С. Организация технического обслуживания, ремонта и модернизации железнодорожного подвижного состава при гарантированном обеспечении безопасности движения / С.С. Конышев, Д.Ю. Лукс, М.А. Козарезова // VI международный форум «Безопасность на транспорте»: сборник докладов. — СПб., 2016. — С. 83-86.
Коссов, В.С. Воздействие длинносоставных поездов на путь / В.С. Коссов, А.А. Лунин, Ю.А. Панин [и др.] // Вестник ВНИИЖТ. — 2016. — Т. 75, № 5. — С. 224-231.
Кудрявцев, H.H. Исследование динамики необреесоренных масс вагонов / Н.Н. Кудрявцев // Сборник научных трудов ЦНИИ МПС. — 1965. — Вып. 287. — С. 190-195.
Кудрявцев, Н.Н. Динамические нагрузки ходовых частей грузовых вагонов / Н. Н. Кудрявцев // Труды ВНИИЖТ. — 1977. — № 572. — 143 с.
Кудрявцев, Н.Н. Определение вертикальных возмущений, вызывающих колебания обрессоренных частей вагона при движении по рельсовому пути
/ Н.Н. Кудрявцев, В.Н. Белоусов, Г.П. Бурчак // Вестник ВНИИЖТ. — 1982. — № 5. — С. 3-9.
Лазарян, В.А. О моделях для исследования взаимодействия подвижного состава и пути / В.А. Лазарян, З.Г. Берман [и др.] // Материалы сетевой научно-технической конференции «Динамика и меры повышения эксплуатационной надежности локомотивов в условиях железных дорого Урала и Сибири». — Омск: Омский ин-т инж. ж.-д. транспорта, 1972. — С. 174-178.
Ли, Х.С. Повышение безопасности движения грузовых поездов на основе мониторинга технического состояния тележки 18-100: диссертация … кандидата технических наук: 05.22.07 / Х.С. Лии. — Омск, 2005. — 185 с.
Лосев, Д.Н. Результаты эксплуатации тихвинских вагонов за пять лет / Д.Н. Лосев // Вагоны и вагонное хозяйство. — 2017. — № 3. — С. 18-19.
Лукс, Д.Ю. Качественный подвижной состав — залог надежной работы вагонного комплекса / Д.Ю. Лукс, И.В. Жуков, А.Н. Михалев, А.С. Макаров // Вагоны и вагонное хозяйство. — 2013. — № 3 (35). — С. 20-21.
Лукс, Д.Ю. Мониторинг динамической нагруженности типовых и инновационных вагонов / Д.Ю. Лукс // IV всероссийская научно- техническая конференция с международным участием «Технологическое обеспечение ремонта и повышение динамических качеств железнодорожного подвижного состава»: сборник трудов. — Омск, 2017. — С. 150-156.
Лукс, Д.Ю. Новые технологии повышают надежность автотормозного оборудования / Д.Ю. Лукс, И.В. Жуков // Вагоны и вагонное хозяйство. — 2013. — № 2(34). — С. 22-25.
Лукс, Д.Ю. Оптимизация гарантийных участков безопасного проследования поездов / Д.Ю. Лукс // Вагоны и вагонное хозяйство. — 2013. — № 1 (33). — С. 20-22.
Лукс, Д.Ю. Оценка динамических качеств грузового вагона, оснащенного тележкой 18-9855 / Д.Ю. Лукс // Известия Транссиба. — 2017. — № 4 (32). — С. 16-25.
Лукс, Д.Ю. Повышение надежности грузовых вагонов в эксплуатации / Д.Ю. Лукс Д.Ю., Жуков И.В. // Железнодорожный транспорт. — 2013. — № 11. — С. 52-54.
Лукс, Д.Ю. Пути совершенствования системы обучения работников вагонного хозяйства / Д.Ю. Лукс // Вагоны и вагонное хозяйство. — 2017. — № 4(52). — С. 4-6.
Лукс, Д.Ю. Совершенствование технологии перевозочного процесса / Д.Ю. Лукс // XII научная конференция «Инновационные проекты и технологии в образовании, промышленности и на транспорте»: сборник трудов. — Омск, 2018. — С. 109-123.
Лукс, Д.Ю. Современные формы организации технической учебы в вагонном хозяйстве / Д.Ю. Лукс, С.С. Кириллова // Вагоны и вагонное хозяйство. — 2016. — № 1(45). — С. 20-25.
Лукс, Д.Ю. Техобслуживанию нужны новые подходы / Д.Ю. Лукс, Е.П. Челтыгмашев. — РЖД Партнер, 2014.
Лукс, Д.Ю. Тяжеловесное движение: как повысить его эффективность? / Д.Ю. Лукс // Вагоны и вагонное хозяйство. — 2014. — № 2(38). — С. 5-8.
Лукс, Д.Ю. Ужесточить требования к вагонам при подготовке под погрузку / Д.Ю. Лукс // Вагоны и вагонное хозяйство. — 2013. — № 4(36). — С. 12-13.
Методика и организация расчета укрупненных и единичных расходных ставок в условиях структурной реформы ОАО «РЖД»: Распоряжение ОАО «РЖД». — 2008. — № 26р.
Методика распределения затрат инфраструктуры ОАО «РЖД»: Распоряжение ОАО «РЖД». — 2008. — № 540р.
Мещерин, Ю.В. О рессорном подвешивании тележек грузовых вагонов / Ю.В. Мещерин // Вагоны и вагонное хозяйство. — 2016. — № 2 (46). — С. 33¬35.
Минжасаров, М.Х. Повышение динамических качеств локомотива совершенствованием буксовой ступени рессорного подвешивания: диссертация … кандидата технических наук: 05.22.07 / М.Х. Минжасаров. — Омск, 2016. — 166 с.
Морчиладзе, И.Г. Совершенствование и модернизация буксовых узлов грузовых вагонов / И.Г. Морчиладзе, А.М. Соколов // Железные дороги мира. — 2006. — № 10. — С. 59-64.
Налабордин, Д.Г. Оценка влияния уровня надежности и безопасности грузовых вагонов на параметры системы их технического обслуживания и ремонта: диссертация … кандидата технических наук: 05.22.07 / Д.Г. Налабордин. — Чита, 2015. — 209 с.
Нарышкин, В.Н. Подшипники качения: Справочник-каталог / В.Н. Нарышкин, Р.В. Коросташевский. — М.: Машиностроение, 1984. — 280 с.
Нехаев, В.А. Исследование влияния параметров нелинейной системы «вагон-путь» на динамику железнодорожного экипажа / В.А. Нехаев, В. А. Николаев, Д. Ю. Лукс // Известия Транссиба. — 2017. — № 3(31). — С. 69- 78.