Цикл статей:
Глава 1 — Повышение безопасности на железнодорожных переездах на основе совершенствования управления автоматической переездной сигнализацией
Глава 2 — Мероприятия по повышению безопасности и снижению аварийности на железнодорожных переездах
Глава 3 — Разработка и исследование системы информативных признаков координаты поезда
Глава 4 — Разработка вычислителя координаты и скорости поезда с корректирующим алгоритмом
В основе вычислителя координаты поезда на УП к переезду лежит формирование уравнения, позволяющего вычислять координаты поезда в текущий момент времени, обладающего инвариантными свойствами и позволяющего оперативно корректировать вид уравнения с целью минимизации ошибки при верификации вычисленной и реальной координаты. Под инвариантностью в данном разделе понимается относительная нечувствительность точности определения координаты к изменению некоторых основных возмущений, воздействующих на параметры РЦ.
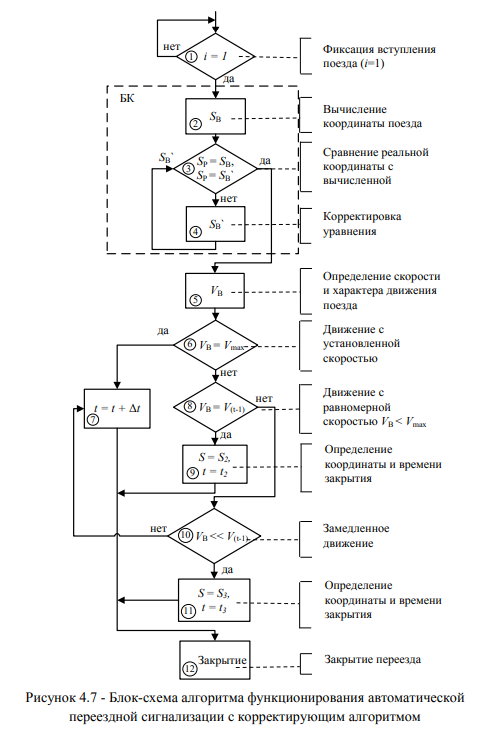
К настоящему времени известно устройство управления АПС с уравнением координаты, сформированном при постоянных значениях первичных параметров РЦ, а именно: удельного сопротивления РЛ, погонной емкости, а также сопротивления ограничения тока на входе РЛ и сопротивления нагрузки РЦ УП [8588]. Гипотеза о постоянстве значений первичных признаков несостоятельна из-за того, что первичные параметры РЛ непрерывно изменяются, вследствие механических и погодных влияний, что приводит к нарушению соответствий вычисленных и текущих координат поезда при постоянных значениях первичных параметров. Ошибка, которая при этом появляется, со временем увеличивается. Вычисленная при неправильной координате скорость неточная, и неправильно определенная координата закрытия переезда приводит к нарушению БДП. Следовательно, метод определения координаты, представленный в работах [85-88], не может гарантировать безопасность движения АТС и поездов на переездах. Поэтому актуальна разработка вычислителя координаты поезда на УП к переезду с множеством информативных признаков, характеризующих координаты поезда [89], и с самонастраивающимся корректирующим алгоритмом, который позволяет, сравнивая вычисленную координату с текущей, рекуррентно корректировать вид и сложность уравнения координаты поезда и повысить точность определения координаты и, соответственно, — скорость поезда.
Определение вида и сложности уравнения вычислителя координаты
поезда
Важнейшей характеристикой сложных систем, к которым относится АПС, является динамичность и нестационарность процессов, характеризующих с течением времени изменение условий работы, параметров первичного датчика. Для управления такими системами, функционирующими в условиях нестационарных процессов, в системах автоматического управления (САУ), как правило, используется адаптивная система (АС) управления [90-93], структурная схема которой приведена на рис. 4.1.
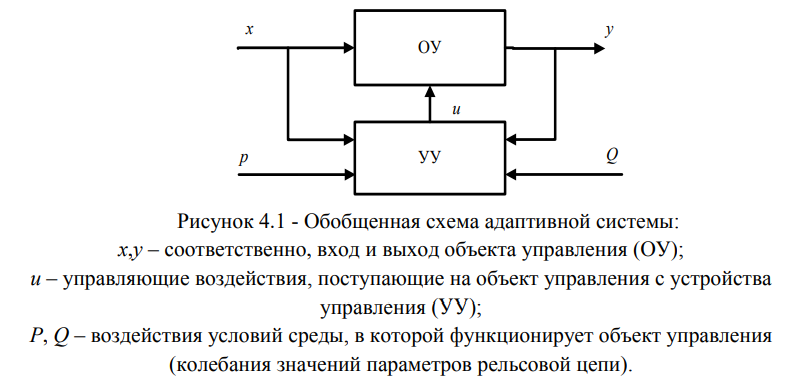
В общем случае адаптивная система классифицируется по различным признакам в зависимости от условий, цели и задачи, решаемых АС [94-96]. Относительно целей и задач, раскрытых в предыдущих главах, рассмотрим два класса АС.
Первый класс характеризуется тем, что в начальной фазе функционирования системы накапливается информация для построения обучающейся системы к изменяющимся параметрам.
Функционирование АСИ осуществляется в двух режимах: обучения и управления. Первый режим — сбор статистической информации и ее обработку — осуществляет стратегический идентификатор. Оперативный идентификатор предназначен для сбора и оценки параметров в текущем временном интервале и для корректировки уравнения вычислителя координат в соответствии с реальной координатой поезда. Наиболее приемлемы в данном случае корректировки уравнения итерационным алгоритмом, обладающим достаточным быстродействием и квазивариантным к ошибкам в исходных данных.
Информационно-управляющую систему управления АПС можно рассматривать как частный случай адаптивных систем с идентификатором. Тогда на первом этапе обучения системы, с использованием обучающей выборки, синтезируется первоначальное уравнения вычислителя координат поезда, а затем в процессе функционирования уравнение корректируется.
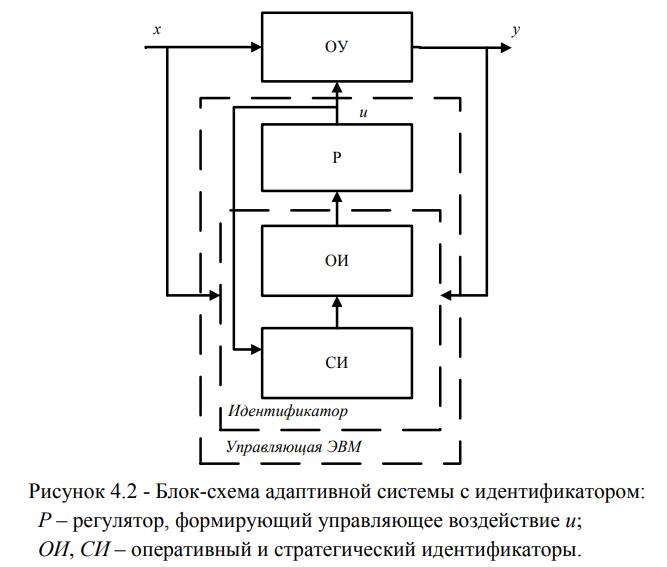
Другой класс необходим для систем, характеристика или условия работы которых нестационарны и изменяются в процессе функционирования, и обучение в начальной стадии создания системы не обеспечивает ее нормальное функционирование. Поэтому необходим непрерывный текущий контроль выходной информации и оперативная коррекция управляющего воздействия с адаптацией уравнения координаты поезда. Этот класс относится к самонастраивающимся системам и принадлежит к адаптивным системам с идентификатором (АСИ), блок-схема которого представлена на рис. 4.2.

Каждая координата представляет собой отрезок пути участка приближения и имеет числовое значение длины, и каждой длине соответствует образ, состоящий из множества информативных признаков — входных электрических параметров рельсового четырехполюсника. Таким образом, весь участок приближения составляет множество образов, каждый из которых обладает некоторыми общими свойствами, а соседние образы отличаются хотя бы значением одного признака. При этом, задача распознавания координат поезда рассматривается как вычисление координаты, используя априорно определенное уравнение, аргументами которого являются измеренные признаки и проверка ошибки вычисления координат, и, если ошибка превышает допустимое значение, то корректируется полином уравнения координаты [97, 98].






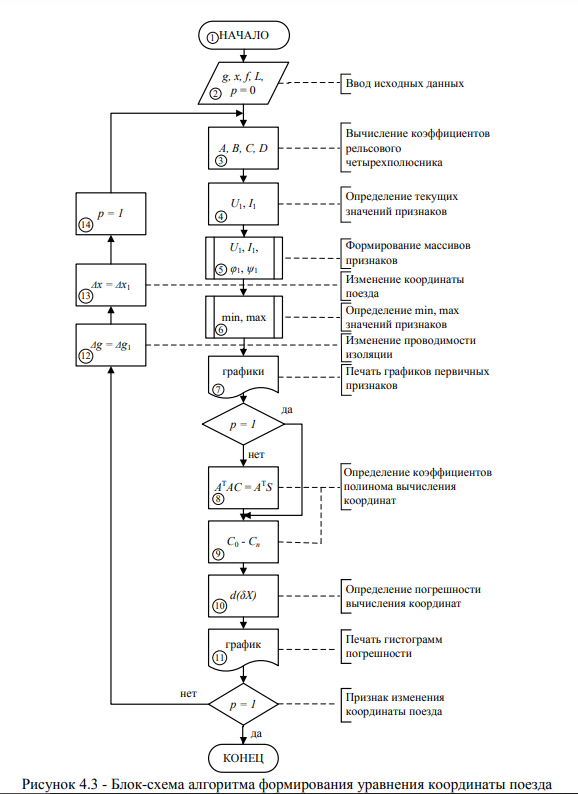
Шаг 7. Решение системы несовместных переопределенных уравнений координат поезда.
Шаг 8. Нахождение коэффициентов полинома уравнения координаты поезда.
Шаг 9. Определение относительной погрешности определения координат поезда.
Шаг 10. Печать графиков результатов исследований погрешностей.
Шаг 11. Изменение признака цикла по проводимости изоляции.
Шаг 12. Изменение значений проводимости изоляции.
Шаг 13. Изменение значений координаты шунта.
Шаг 14. Изменение признака окончания исследований.
Учет изменения проводимости изоляции РЛ при определении коэффициентов полинома РФ позволяет обеспечить нечувствительность к воздействию возмущающего фактора — проводимости изоляции.
Реализация уравнения координаты поезда


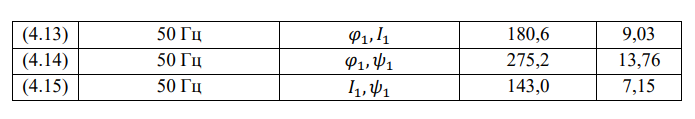
Разработка принципа корректировки уравнения координаты поезда при
расстройке алгоритма распознавания
Если система распознавания координат поезда работает в стационарной среде, т.е. при условиях, когда первичные параметры рельсовой линии не изменяются, то она обучается распознаванию по статистическим характеристикам признаков с помощью учителя. Например, коэффициенты полинома можно вычислить приемами из теории многомерной аппроксимации решением системы уравнений. После завершения процесса обучения коэффициенты отражают статистическую структуру первичных параметров, которые теперь считаются неизменными или «замороженными».
Чаще всего окружающая среда рельсовых линий изменчива из-за динамических воздействий поездов и климатических условий, поэтому значения первичных параметров являются нестационарными, и это приводит к расстройке полинома уравнения координаты поезда. В таком случае методы обучения с учителем могут применяться только для коротких временных промежутков, т.к. система не обладает свойствами отслеживания статистических вариаций первичных параметров, т.е. информативных признаков. Для устранения этого недостатка необходимо адаптировать параметры полинома к вариациям входного сигнала в режиме реального времени при вступлении поезда на участок контроля.
Известно, что чем выше адаптивные способности системы, тем более устойчивой будет ее работа в нестационарной среде [106]. При этом необходимо отметить свойство зависимости сложности уравнения координаты поезда и устойчивости системы, иногда она приводит к совершенно противоположному результату. Вычислительные эксперименты на математической модели показали, что с увеличением степени полинома уравнения вычисления координат свыше третьей, чувствительность к изменению первичных параметров становится чрезмерно высокой. Так, например, 10% наиболее влияющего параметра РЛ приводит к 30 % увеличению погрешности определения координат. Поэтому в исследованиях автор остановился на квадратичных функциях полинома уравнения вычислителя координат поезда.
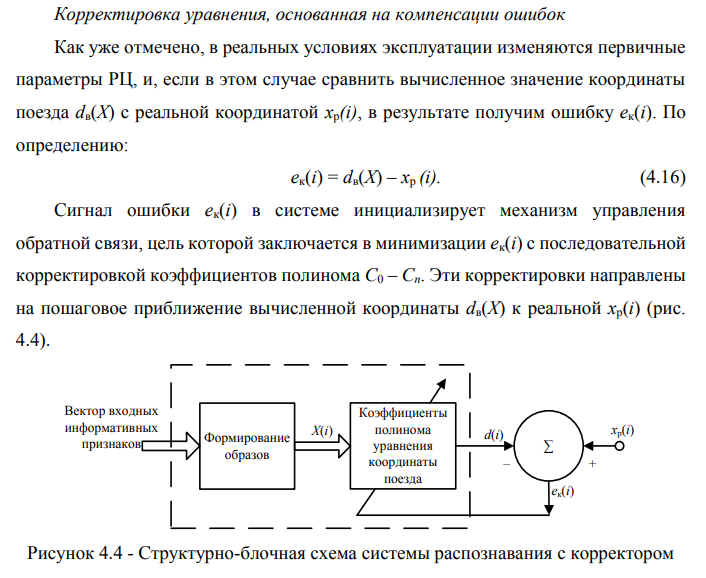



На рисунке видно, что обучение на основе коррекции ошибок — это пример замкнутой системы с обратной связью. Из теории управления известно, что устойчивость такой системы определяется параметрами обратной связи.
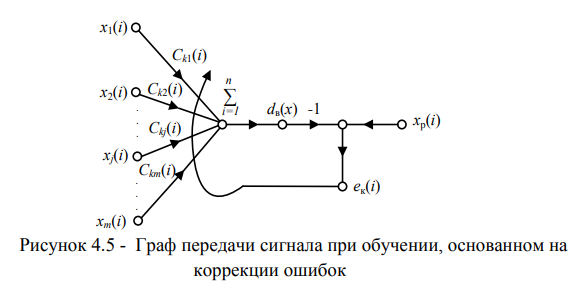
Понятие обратной связи характерно для динамических систем, в которых входной сигнал (первичный параметр) оказывает влияние на выходной сигнал [108]. В нашем случае обратная связь является корректирующей цепочкой коэффициентов полинома уравнения координаты поезда. На рис. 4.6 показан граф прохождения сигнала в системе с обратной связью для одного коэффициента полинома.

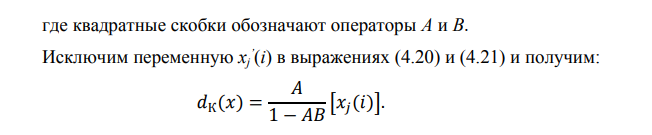

Реализация принципа корректировки уравнения координаты поезда




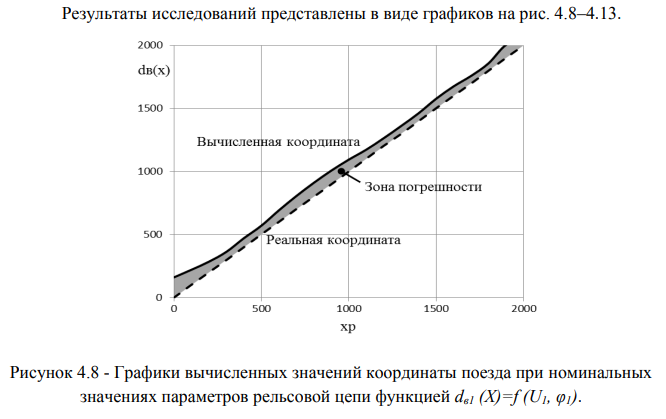
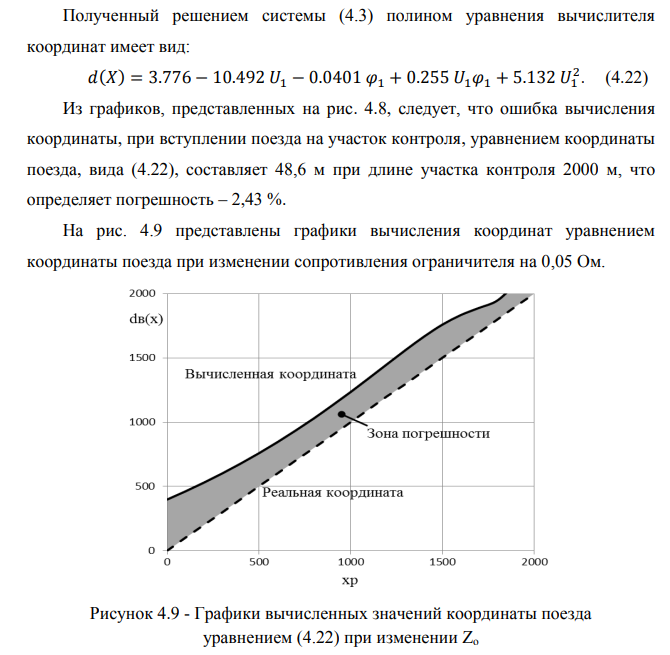

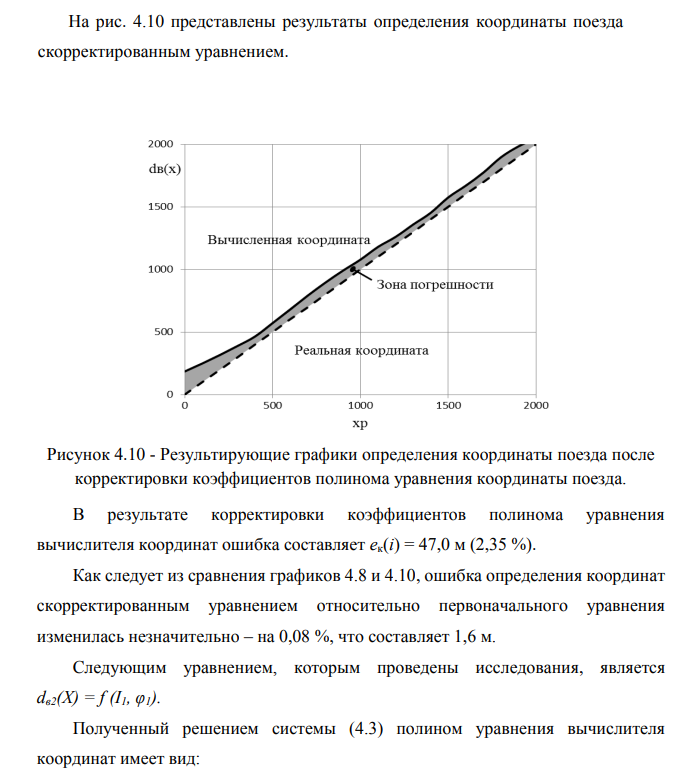
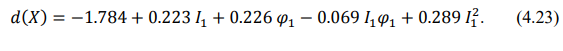
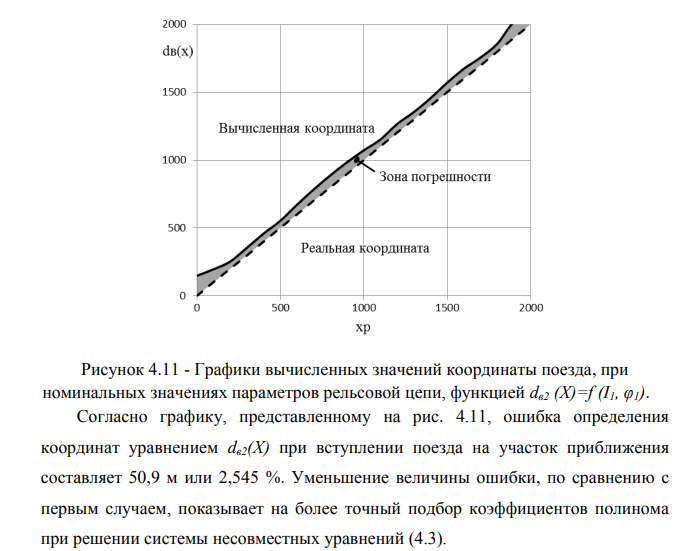
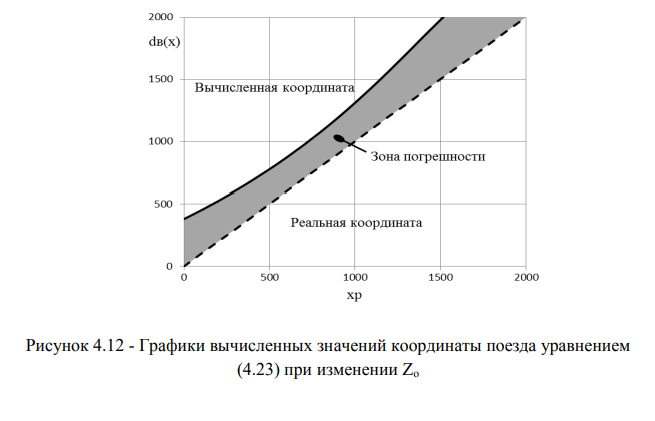
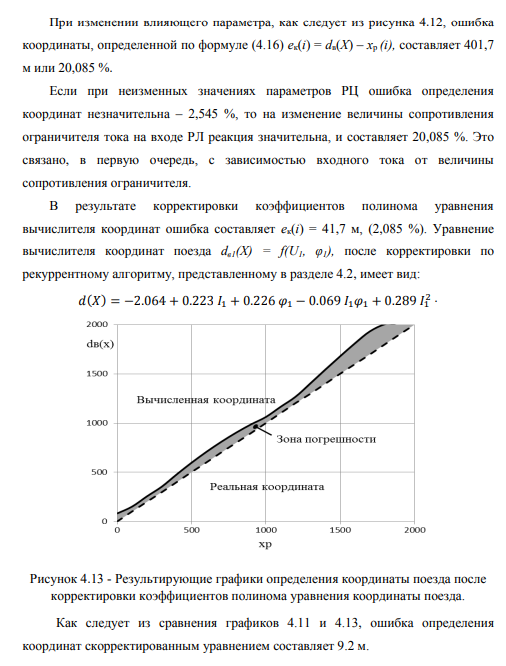
Анализ результатов исследований


Выводы по четвертой главе
- Исследования показали, что в прикладных задачах, к которым относится задача распознавания координат поезда, как правило, достаточно использовать уравнения вычислителя с квадратичными членами. Вычислительные эксперименты на математической модели показали, что с увеличением степени полинома уравнения вычисления координат свыше третьей, чувствительность к изменению первичных параметров рельсовой цепи становится чрезмерно высокой. Изменение на 10 % наиболее влияющего параметра РЛ приводит к 30 % ухудшению точности вычисления координат.
- Разработанная процедура определения коэффициентов полинома вычислителя координат поезда с множеством информативных признаков посредством решения системы условных уравнений, где каждому уравнению соответствует определенная координата поездного шунта, позволяет учитывать все возможные значения проводимости в заданном диапазоне ее изменения и обеспечить относительную инвариантность уравнения вычислителя координат поезда к изменению проводимости изоляции в пределах от 2 См/км до 0,1 См/км.
- С использованием четырех первичных признаков, вида уравнения координаты поезда и машинных алгоритмов формирования уравнений координат, реализованы 12 уравнений координат, из которых 6 уравнений — при частоте тока опроса датчика 25 Гц и 6 уравнений — при частоте 50 Гц. Ошибка вычисления координат поезда с полученными уравнениями составляет от 4,5 % до 22,1 %, в зависимости от сочетаний признаков в квадратичном полиноме.
- Предложенная методика корректировки уравнения координат поезда, основанная на коррекции ошибок вычисления координат, сравнением вычисленного значения координаты поезда с реальной, и на минимизации результирующей ошибки рекуррентной вычислительной процедурой, позволяет, путем внутренней логики развития, изменять вид уравнения (максимально упростить) и корректировать коэффициенты полинома уравнения вычислителя координат.
- Разработанный алгоритм апробирован на двух примерах реализации уравнения вычислителя координат поезда, и оказалось, что рекуррентный алгоритм корректировки уравнения, предложенный в работе, позволяет обеспечить минимизацию ошибки, появляющуюся из-за нестационарности среды, приводящей к изменению параметров многопараметрического датчика, а, следовательно, и информативных признаков. Предложенный алгоритм обладает еще одним положительным свойством, а именно, процедура корректировки позволяет изменить вид уравнения, его сложность и уточнить коэффициенты, полученные приближенным решением системы уравнений, из-за его переопеределенности, что существенно уменьшает погрешность вычисления координаты поезда.
Список литературы
- Патент RU 2169678 Устройство для переездной сигнализации / Мохонько В.П., Тарасов Е.М., Белоногов А.С., Куров М.Б., Гуменников В.Б., Тарасова Е.В. — заявл. 16.06.2000г., опубл. Б.И. 2001г., №18.
- Герус, В.Л. Разработка информационно-управляющей системы переездной сигнализации с многопараметрическим датчиком координаты поезда / В.Л. Герус, Е.М. Тарасов, А.Е. Тарасова // Перспективные информационные технологии (ПИТ 2017) : труды междунар. науч.-техн. конф. — Самара, 2017. — С. 742-745.
- Антонов В.Н. Адаптивные системы автоматического управления : Учеб. пособие / В.Н. Антонов, А.М. Пришвин, В.А. Терехов, А.Э. Янчевский : под ред. проф. В.Б. Яковлева. — Л.: изд-во Ленингр. ун-та, 1984. — 204 с.
- Бессонов, А.А. Методы и средства идентификации динамических объектов / А.А. Бессонов, Ю.В. Загашвили, А.С. Маркелов. — Л.: Энергоатомиздат. Ленингр. Отд-ние, 1989. — 280 с.
- Льюнг, Л. Идентификация систем. Теория для пользования / Л. Льюнг. — М.: Наука. Гл. ред. физ.-мат. лит., 1991. — 432 с.
- Чинаев, П.И. Самонастраивающиеся системы. Справочник / П.И. Чинаев. — Киев: Наукова Думка, 1969. — 528 с.
- Anderson, T.W. On asymptotic distributions of estimated parameters of stochastic difference equations / T.W. Anderson // Ann. Math. Stat. — 1959. — Vol. 30. — P.676-687.
- Andersson, P. Adaptive forgetting in recursive identification through multiple models / P. Andersson // Int. J. Control — 1985. — Vol. 42. — P.1175-1194.
- Anscombe, F.J. The examination and analysis of residuals / F.J. Anscombe, J.W. Turkey // Tech-nometric — 1963. — Vol. 5. — p.141-160.
- Герус, В.Л. Кластеризация путей подгорочного парка для автоматического определения координат отцепов / В.Л. Герус, Д.В. Железнов, Е.М. Тарасов, М.В. Трошина // Наука и образование транспорту : материалы VIII междунар. науч.- практ. конф. — Самара, 2015. — С. 112-115.
- Герус, В.Л. Методика определения решающей функции в задаче вычисления координаты динамического объекта / В.Л. Герус, Е.М. Тарасов, С.В. Копейкин // Информационные технологии и нанотехнологии (ИТНТ-2016): сб. материалов междунар. конф. и молодежной школы — Самара, 2016.
- Ту, Дж. Принципы распознавания образов / Дж. Ту, Р. Гонсалес. — М.: Мир, 1978. — 412 с.
- Потапов, А.С. Распознавание образов и машинное восприятие: общий подход на основе принципа минимальной длины описания / А.С. Потапов. — С-Пб.: Политехника, 2007. — 548 с.
- Ивахненко, А.Г. Техническая кибернетика. Системы автоматического управления с приспособлением характеристик / А.Г. Ивахненко. — Киев.: Техника, 1962. — 422 с.
- Тарасова, А.Е. Разработка структуры информационной системы для определения скорости скатывающегося вагона / А.Е. Тарасова, Е.М. Тарасов //
Теория и практика научных исследований: материалы Междунар. молодежной науч.-практ. конф. — Астана, Казахстан, 2016. — С.-19-24. - Корн, Г. Справочник по математике для научных сотрудников и инженеров / Г. Корн, Т. Корн. — М.: Наука, 1968. — 720с.
- Бронштейн, И.Н. Справочник по математике для инженеров и учащихся ВУЗов / И.Н. Бронштейн, К.А. Семендяев. — М.: Наука, 1986. — 544с.
- Лаврентьев, М.А. Методы теории функции комплексного переменного / М.А. Лаврентьев, Б.М. Шабат. — М.: Наука. Гл. ред. физ.-мат. лит, 1987. — 688с.
- Цыпкин, Я.З. Адаптация и обучение в автоматических системах / Я.З. Цыпкин. — М.: Наука, 1968.
- Tapia, R.A. Nonparametric Probability Density Estimation / R.A. Tapia, J.R. Thompson. — Baltimore: The Johns Harpkins University Press, 1978.
- Хайкин, Саймон. Нейронные сети: полный курс, 2-е изд., испр.; пер. с англ. — М.: ООО « И.Д. Вильямс», 2006. — 1104 с.
- Хлытчиев, С.М. Основы автоматики и автоматизации производственных процессов: Учебник для вузов связи / С.В. Хлытчиев, А.С. Ворожцов, И.А. Захаров. — М: Радио и связь, 1985. — 288 с.
- Герус, В.Л.. Использование решающих функций для определения координаты поезда на участке приближения / В.Л. Герус, А.Е. Тарасова // Наука и образование транспорту: материалы X междунар. науч.-практ. конф. — Самара, 2017. — Т. 1 — С.215-218.
