Теоретическое исследование процесса восстановления профиля катания колесных пар повышенной твердости

Расчет температур

При восстановлении обточкой обода колеса, возникающие на поверхно­стях инструмента температуры, определяют работоспособность инструмента и ограничивают производительность обработки [8]. Необходимым и достаточным условием оптимальности протекания процесса обточки колесных пар, по мнению ряда авторов [4, 10], является реализация в зоне резания оптимальной температу­ры, которая составляет «870°С. Работа колесотокарных станков в производствен­ных условиях с использованием оптимальной температуры резания или темпера­туры формоустойчивости [8] является наиболее целесообразной.

К расчету температур в режущем инструменте предъявляются особо высо­кие требования. Это связано с тем, что небольшие ошибки, допущенные при рас­чете температуры, могут привести к весьма существенным погрешностям опреде­ления соответствующей этой температуре скорости резания. В использовавшихся ранее методиках [9, 10, 11] при расчете температуры деформации не учитывалось влияние скорости деформации, деформации и температуры на касательные на­пряжения (предел текучести), не учитывается сама величина конечных деформа­ций (конечный истинный сдвиг), равная относительному сдвигу. Температура пе­редней поверхности считается пропорциональной корню квадратному из крите­рия Ре. В действительности это не так. В частности, экспериментальными дан­ными исследователей [12, 13] доказано, что в области высоких температур рост температуры с увеличением критерия Ре замедляется, причем тем в большей сте­пени, чем выше температура. Это свидетельствует об уменьшении предела теку­чести на передней поверхности с ростом температуры, то есть о разупрочнении обрабатываемого материала. Учет разупрочнения материала при повышении тем­пературы является обязательным условием для повышения точности расчета тем­пературы.

При расчете температуры задней поверхности не учитывался источник те­пла на участке застойной зоны. Учет застойной зоны существенно влияет на рас­пределение температуры на фаске износа задней поверхности. Не учитывается и возможное разупрочнение материала на задней поверхности, которое может иметь место при высоких скоростях резания и большой ширине фаски износа.

В связи с этим значительный практический и теоретический интерес пред­ставляет создание программ, позволяющих выполнить анализ токарной обработки железнодорожных колесных пар теоретически, с помощью расчетов на ЭВМ. Ре­шение этой задачи потребовало разработки методики расчета температур и на­пряжений на поверхностях режущего инструмента, обоснования выбора теорети­чески определяемых факторов, тесно связанных с изнашиванием и деформацией режущих лезвий, разработки методики расчета сил резания и отклонений обрабо­танной поверхности. При расчете сил, температуры и напряжений на поверхностях режущего лезвия использовался термомеханический подход.

Расчет и анализ сил резания при прямоугольном точении чашечным резцом и резцом с прямолинейной режущей кромкой с закругленной вершиной

Рассмотрим точение чашечным резцом или криволинейной частью резца с закругленной радиусом г вершиной и геометрией в плоскости стружкообразования по рис.3.1.

Для расчета сил при прямоугольном точении инструментом с криволиней­ной режущей кромкой, рассмотрим малый отрезок режущей кромки Д/ (рис. 3.1), считая его прямолинейным и наклоненным к направлению подачи под углом в плане ср_х. Приращение силы на передней поверхности в горизонтальной плоско­сти и приращение нормальной силы на задней поверхности направлены перпен­дикулярно отрезку режущей кромки Д/. Эти силы могут быть вычислены по ме­тодике, описанной в [8, 14]:

На рис. 3.14. показаны проекции приращений этих сил на оси у и х.

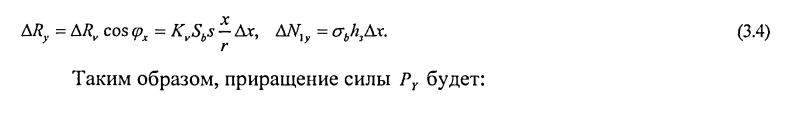
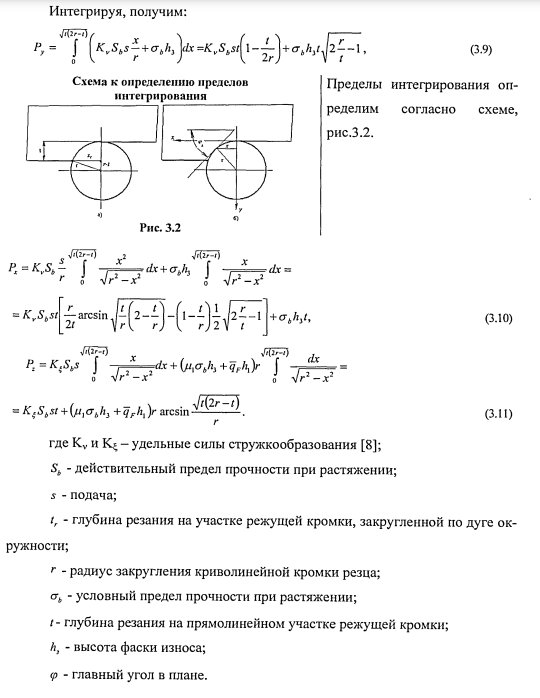
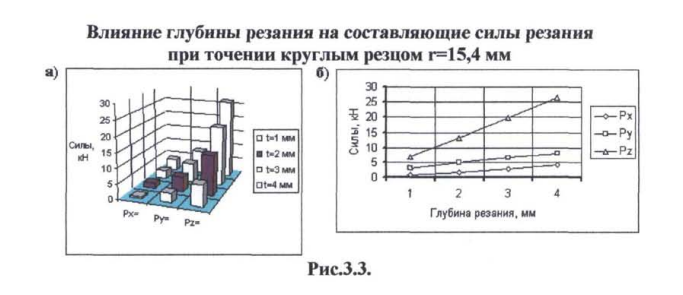
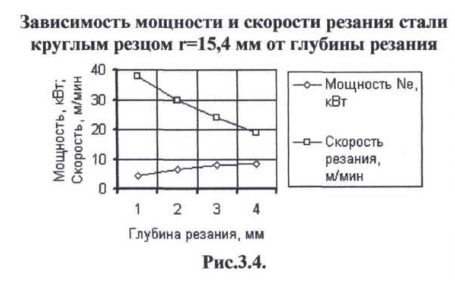
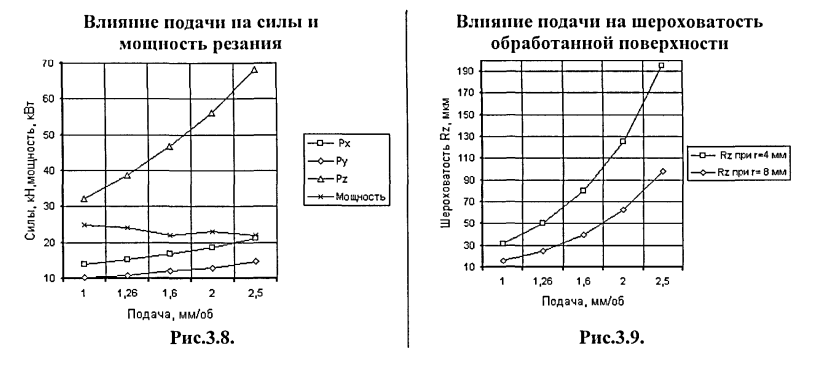
С увеличением глубины ре­зания при точении чашечным рез­цом возрастает максимальная толщина срезаемого слоя, проис­ходит возрастание силы резания (рис.3.3) и, следовательно, увели­чиваются температуры передней,

задней поверхностей и температура резания. Для постоянства оптимальной тем­пературы (температуры формоустойчивости) увеличение толщины срезаемого слоя необходимо компенсировать соответствующим снижением скорости резания (рис.3.4), что свидетельствует о целесообразности использования чашечного рез­ца для чистового прохода.

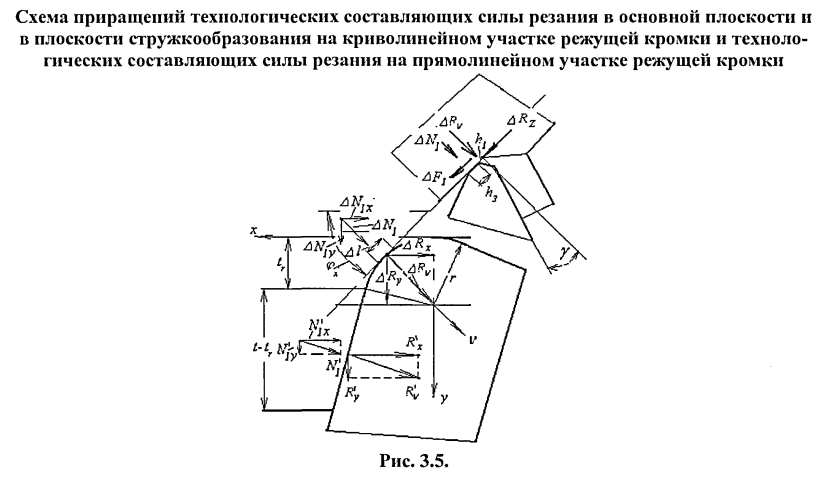
Проводя аналогичные рассуждения для «призматического» резца (рис. З.5.), имеющего участок криволинейной кромки — закругления вершины резца в плане, и участок прямолинейной кромки, расположенной под углом в плане ср, силы резания могут быть вычислены суммированием сил, вычисленных для каж­дого из названных участков:

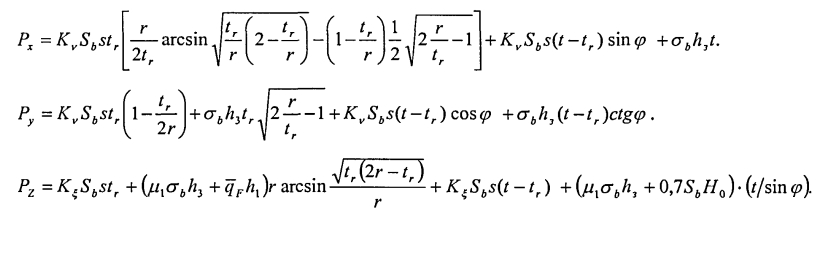
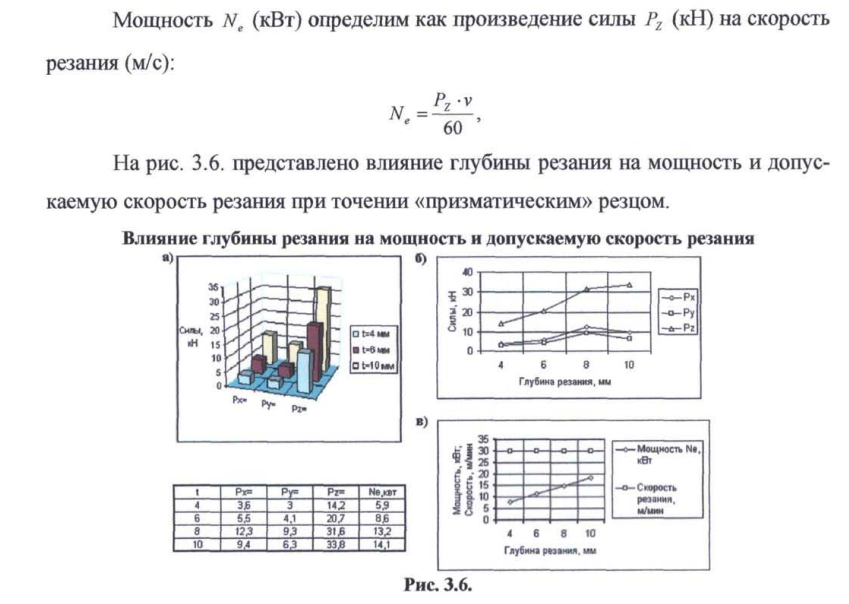
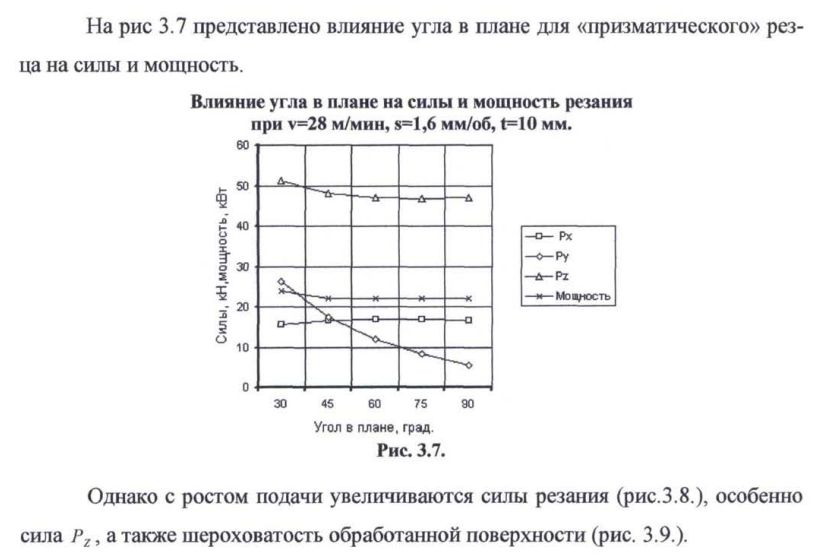
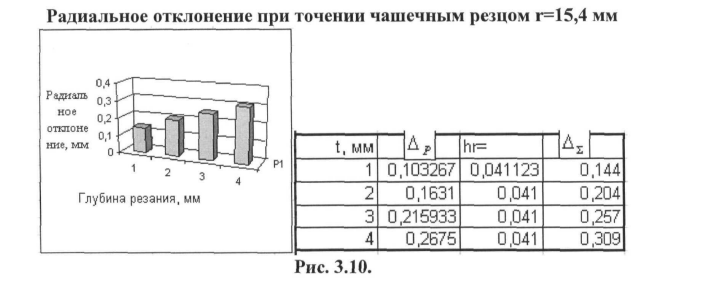
Расчет отклонений поверхности колеса из-за сил резания и износа резца

При точении чашечным резцом, чтобы отклонение обработанной поверх­ности было в пределах нормы (до 0,2 мм) глубина резания при чистовом проходе не должна превышать 2 мм (рис.3.10).

Расчет и анализ температур передней и задней поверхно­стей резца при восстановлении профиля катания колесной пары

Рассмотрение закономерностей распределения теплоты имеет большое значение для понимания физической сущности для понимания физической сущ­ности и для разработки универсальных и точных методов расчета характеристик процесса резания. Значительный вклад в исследовании оценки температур в ре­жущем инструменте при обработке колес как численными методами так и экспе­риментально внес д.т.н. профессор кафедры «Теплотехника и теплосиловые уста­новки » ПГУПС И.Г. Киселев.

В работах проф. Киселева И.Г. предложен общий подход к рассмотрению и решению задач теплофизики, возникающих при ремонте колесных пар [15, 16, 17]. Теоретически краевые задачи теплопроводности сформулированы для любых объектов с различными условиями теплообмена на границах. При решении ли­нейных и нелинейных краевых задач теплопроводности применительно к состав­ным телам сложной формы (бандажное колесо, сборный режущий инструмент и др.) предпочтение было отдано методу последовательного энергетического балан­са.

При анализе температурных полей резца отмечается, что преобладающим является тепловой поток, поступающий с передней поверхности инструмента. Часть этого потока попав в резец, отводится через заднюю поверхность инстру­мента в колесо и окружающую среду. Это приводит к перемене знака радиального градиента температуры, близко расположенной к этой поверхности резца.

В настоящей работе для получения более точных данных о распределении температур на рабочих поверхностях инструмента при восстановлении профиля колеса использован термомеханический подход, учитывающий изменение свойств обрабатываемого материала при высоком уровне скорости деформации, изменяющихся деформациях и температурах, характерных для процесса восста­новления.

Тепловые потоки и температура контактных слоев передней и задней по­верхностей режущего инструмента оказывают значительное влияние на его со­стояние. Резкое изменение этих параметров в начале процесса резания, их высо­кий уровень и различные скорости прогрева инструмента приводят к возникнове­нию дополнительных термических напряжений. Частые повторные действия тер­мических напряжений ведут к термоусталостному разрушению резцов. В основу расчета температуры на поверхностях инструмента положен тер­момеханический подход, описанный в [8] с использованием методов подобия для резания материалов, разработанными С.С. Силиным [10]. На основе анализа уравнения баланса механической и тепловой энергии при резании металлов С.С. Силин использует в расчетах безразмерные комплексы (критерии подобия)

При расчете температур на рабочих поверхностях режущего инструмента решалась задача теплопроводности, описываемая уравнением Фурье (3.12) с гра­ничными условиями всех четырех видов. При этом определяющими являются
граничные условия со стороны передней и задней поверхностей резца, контакти­рующих с деталью и стружкой.

Определяющие уравнения для идеально пластического и упрочняемого материалов могут рассматриваться как упрощенные частные случаи более общего определяющего уравнения [8], отражающего влияние на предел текучести и де­формации, и скорости деформации, и температуры. Примером такого обобщенно­го определяющего уравнения служит функция вида

Для условий резания металлов представляет особый интерес учет измене­ний температуры, вызванных деформацией. Наиболее просто приращение темпе­ратуры связано с деформацией в адиабатических условиях, т.е. в таких условиях, когда вся теплота остается в том объеме материала, в котором оно выделилось при деформации.

Поскольку в большинстве случаев перетоками теплоты в широкой области деформаций и оттоками теплоты из этой области в деталь можно пренебречь, то условия деформации материала в этой области могут быть охарактеризованы как адиабатические, т.е. без теплообмена деформируемой частицы с окружающим ее металлом. В этом случае с ростом текущего значения деформации соответственно увеличивается и температура. При допущении о постоянстве скорости деформации два последних со­множителя определяющего уравнения линейно зависимы и уравнение может быть представлено в виде [8].

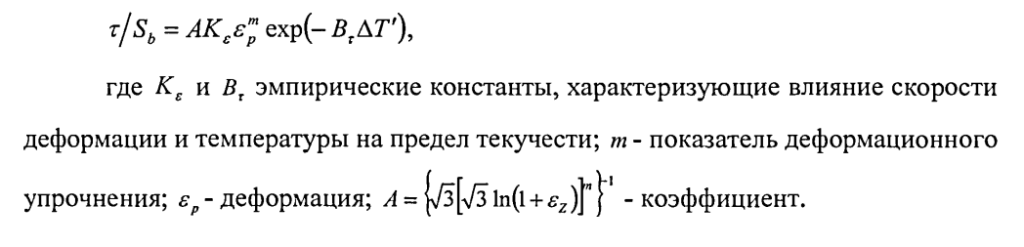
Строки первой матрицы представляют значения источника тепла и стоков, учитывающих разупрочнение материала под действием температуры.

В первом столбце матрицы указаны значения источника тепла, плотность теплового потока которого соответствует максимальному значению предела теку­чести на передней поверхности. Столбцы второй матрицы содержат значения длин соответствующих ин­тервалов. Произведение матриц дает распределение температуры по длине кон­такта стружки с передней поверхностью резца.

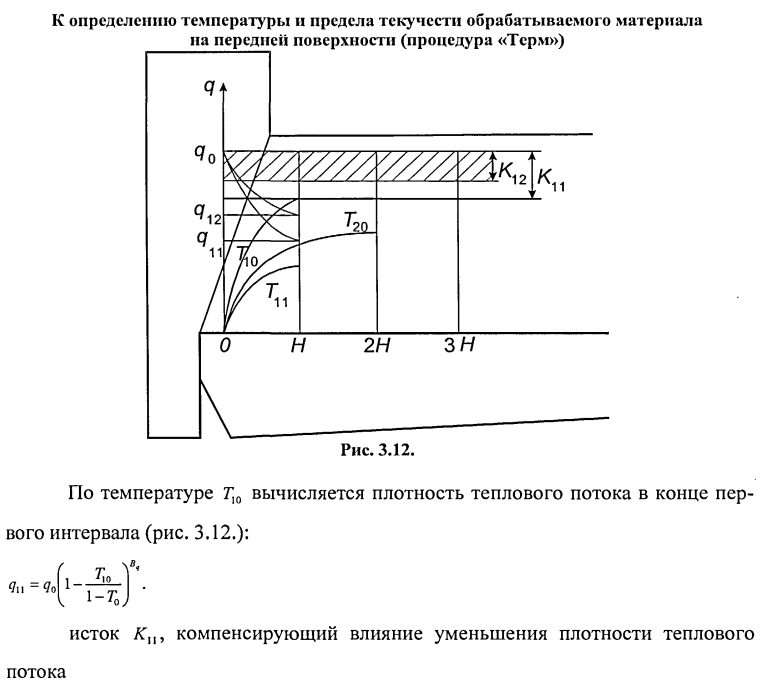
Итерации повторяются до получения устойчивого результата. Как правило, для этого достаточно 3-4 итераций. Кроме того, сходимость и устойчивость ре­шения зависит от длины интервала. Первые интервалы должны быть достаточно малыми, так как температура на этом интервале возрастает быстро. Благодаря та­кому подходу, учитывающему зависимость плотности теплового потока от темпе­ратуры, нелинейное дифференциальное уравнение теплопроводности сводится к линейному на каждом из интервалов и на каждой итерации.

На следующем интервале добавляется еще один сток и т.д.

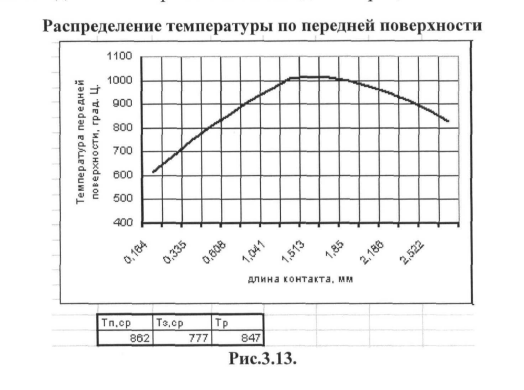
Зависимость температуры от координаты передней поверхности представ­ляется в виде графика (рис. 3.13.).

Аналогично рассчитывается и температура задней поверхности. Здесь ите­рации предусмотрены только для участка задней поверхности застойной зоны, для которого выделены 8 интервалов представленных на рисунках 3 и 4 приложе­ния 2.

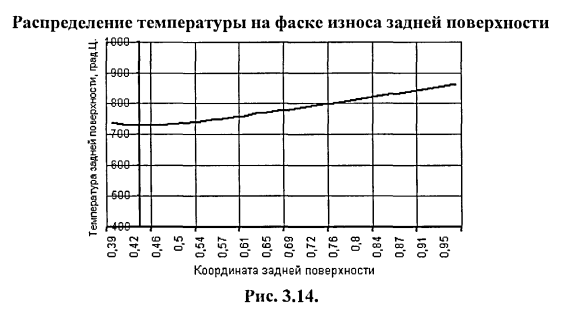
Зависимость температуры задней поверхности от координаты задней по­верхности представлена в виде графика (рис.3.14).

Температура более 700° С на режущей кромке достигается под воздействи­ем источника тепла, расположенного на участке застойной зоны. Поскольку плот­ность теплового потока на участке застойной зоны значительно выше, чем на фаске износа, температура на фаске износа на некотором участке не только не возрастает, но напротив даже несколько уменьшается, достигая минимума, и только затем увеличивается. Благодаря этому заточка на задней поверхности фас­ки первоначального притупления величиной около 0,2 — 0,3 мм практически не вызывает повышения температуры или вызывает несущественное повышение температуры. Однако это наблюдается при относительно невысокой скорости ре­зания. Такое первоначальное притупление благоприятно с точки зрения повыше­ния пластической прочности режущего лезвия.

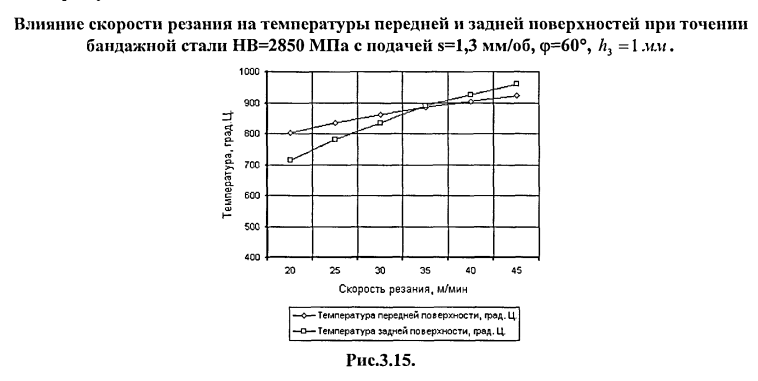
Проанализируем влияние отдельных факторов на расчетные температуры. При постоянных подаче 5 и угле в плане ф и постоянной ширине фаски износа, примерно равной критерию затупления h₃ = 1 мм с ростом скорости резания тем­пературы на передней и задней поверхностях инструмента растут, рис. 3.15.

При этом температура задней поверхности растет быстрее, чем температу­ра передней поверхности. Медленный рост температуры передней поверхности связан с разупрочнением обрабатываемого материала с повышением температу­ры. Если бы теплостойкость инструментального материала и его прочность при высоких температурах были бы выше, чем у реальных сплавов типа Т14К8 или Т5К10, то повышение скорости резания, соответствующее повышению произво­дительности обработки было бы целесообразным. Однако как раз в области по­вышения температуры от 800°С прочностные характеристики режущего лезвия резко снижаются, а вероятность деформаций и последующего катастрофического износа или разрушения (поломки) режущей пластины возрастает.

На прочность и формоустойчивость режущего лезвия оказывают влияние обе температуры: и на передней и на задней поверхностях инструмента. Но в каком соотношении они влияют на работоспособность инструмента? В том соотно­шении, в каком они влияют на температуру резания, или в другом? В работе [8] используется понятие температуры формоустойчивости режущего лезвия, которая кажется более подходящей для характеристики износостойкости и работоспособ­ности режущего лезвия.

Температура формоустойчивости характеризует в среднем температуру внутри режущего лезвия, оказывающую сильное влияние на пределы прочности инструментального материала. Режущее лезвие (клин) прогревается равномерно по сечению в том случае, когда температуры передней и задней поверхностей равны друг другу. В случае неравенства этих температур точки, соответствующие возникновению катастрофического износа (или точки, соответствующие постоян­ной интенсивности изнашивания инструмента) располагаются на кривой, близкой к окружности (рис. 3.16).

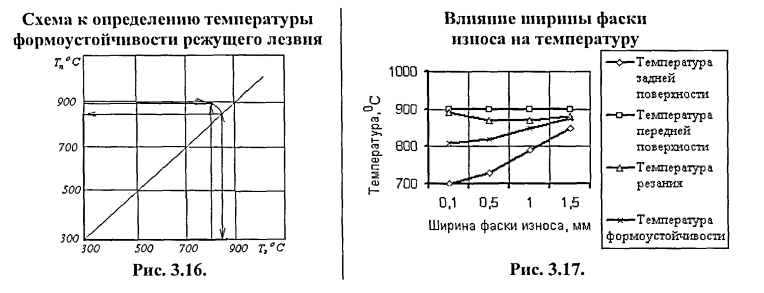
При износе инструмента температура передней поверхности практически постоянна (если существенно не изменяется передний угол в случае образования лунки), а температура задней поверхности, начиная с некоторых небольших зна­чений ширины фаски износа, растет (рис.3.17). Вместе с ней увеличивается и тем­пература внутри режущего клина. Эта тенденция хорошо улавливается темпера­турой формоустойчивости, в то время как температура резания сначала уменьша­ется, а затем практически мало меняется. Следовательно в качестве температур­ного фактора, влияющего на формоустойчивость и износостойкость инструмента следует использовать температуру формоустойчивости, а не температуру резания.

Однако, учитывая, что в работах [18, 19-21] часто используется именно температура резания, приведем данные и об ее изменении.

Основной задачей исследования и оптимизации является повышение про­изводительности [22 — 24] (или достижение наибольшего возможного уровня про­изводительности) при сохранении рационального уровня температуры. Поэтому необходимо выяснить какие факторы способны снизить температуру при посто­янной производительности.

Еще одной задачей является обоснование и выбор температурного факто­ра, наиболее тесно связанного с допускаемыми (рациональными) режимами реза­ния и износостойкостью режущего инструмента. Традиционно в качестве основного температурного фактора использова­лась температура резания, определявшаяся либо экспериментально — методом ее тественной термопары, либо расчетным путем как средняя между температурами передней и задней поверхностей инструмента.

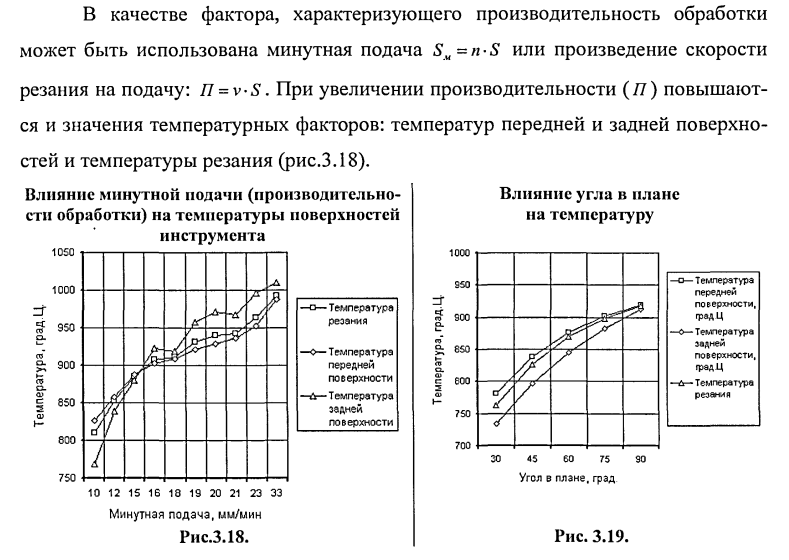
Довольно существенное влияние на температуру оказывает изменение угла в плане (рис.3.19).

Увеличение подачи на оборот при постоянной минутной подаче приводит к снижению температуры. Особенно существенно снижается температура задней поверхности.

Как следует из рис. 3.23, при достаточно больших значениях толщины сре­заемого слоя, характерных для обтачивания железнодорожных колес, температу­ры передней поверхности и резания близки друг к другу. Особенно они близки при точении резцом с небольшой шириной фаски износа. Поэтому в первом при­ближении в качестве характеристики температуры могут использоваться как тем­пература передней поверхности, так и температура резания.

Большое значение имеет переход от температуры, рациональные значения которой, как правило, известны и находятся в достаточно узком диапазоне, к со­ответствующей (рациональной) скорости резания, значения которой могут изме­няться в более широком диапазоне в зависимости от твердости обрабатываемого материала, подачи, угла в плане, переднего угла, ширины фаски износа и других факторов (рис.3.21.).

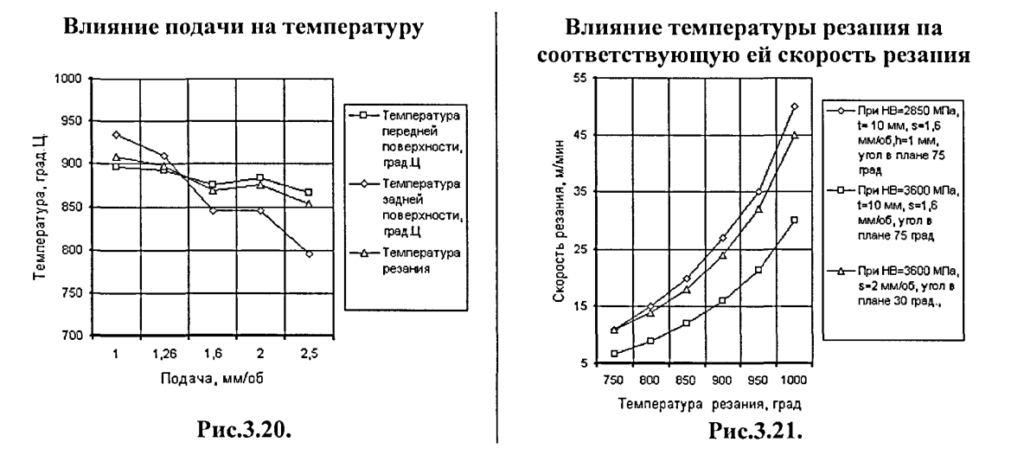
Такой переход может быть выполнен только с помощью достаточно точ­ных расчетов, основанных на термомеханическом подходе.

Зависимости допускаемой скорости от температуры описываются вогну­тыми кривыми (рис. 3.21.). При интенсивных режимах резания, соответствующих повышенным температурам увеличение скорости резания вследствие разупрочне­ния материала все слабее влияет на температуру. При этом создается обманчивое впечатление, заключающееся в том, что поскольку скорость резания слабо влияет на температуру, ее можно повышать. Однако в действительности максимальные и средние температуры передней и задней поверхностей и, следовательно, и темпе­ратура резания должны быть ограничены рациональными значениями, в качестве которых в первом приближении может быть принята «оптимальная температура», рекомендуемая С.С.Силиным — 870 °С, а также полученная в работах кафедры «Технология металлов».

Меньшие углы в плане (например, 30°) могут быть применены при не­больших глубинах резания (рис.3.22).

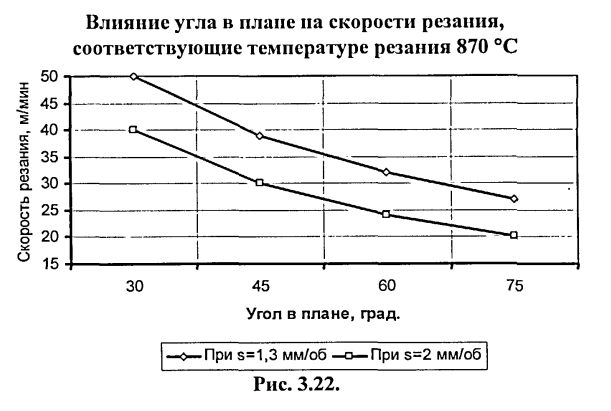
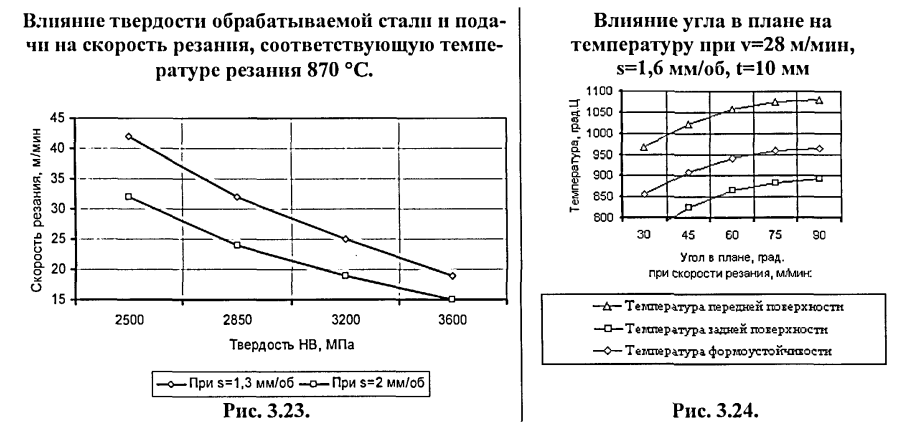
Уменьшение угла в плане существенно снижает температуру (рис. 3.24) при этом скорость резания может быть увеличена (рис З.7.), но увеличивает силу Р_у [25, 26].

Характеристики процесса резания при различном износе инструмента

В связи с отсутствием надежных экспериментальных данных и производ­ственных наблюдений об изнашивании режущих пластин при обработке железно­дорожных колес из колесной стали, близкой по составу к углеродистой стали 60, воспользуемся данными «Сандвик Коромант» (см. табл. 3.2) [27]. Значение стой­кости для скорости 20 м/мин получено экстраполяцией.

В качестве критерия затупления по задней поверхности принята ширина фаски износа 1 мм (см. табл. 3.3). Средние значения интенсивности изнашивания в первом приближении рассчитывались как отношение ширины фаски износа к пути резания.

Значения интенсивностей изнашивания при точении с толстыми срезами (о,25 — 2,5)-10⁶ на порядок больше, чем при точении с тонкими и средними срезами [20]. Это свидетельствует о большой роли пластических деформаций в формоиз­менении и изнашивании режущего лезвия. В связи с этим в качестве температур­ного фактора целесообразно использовать температуру формоустойчивости ре­жущего лезвия.

Пластические деформации режущего клина происходят с тем большей скоростью, чем выше отношение эквивалентных напряжений к допускаемому эк­вивалентному напряжению. Предполагается, что допускаемое эквивалентное на­пряжение зависит от температуры внутри режущего лезвия. В качестве характе­ристики этой температуры нами используется температура формоустойчивости:

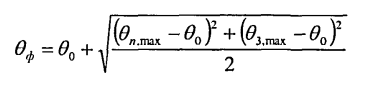
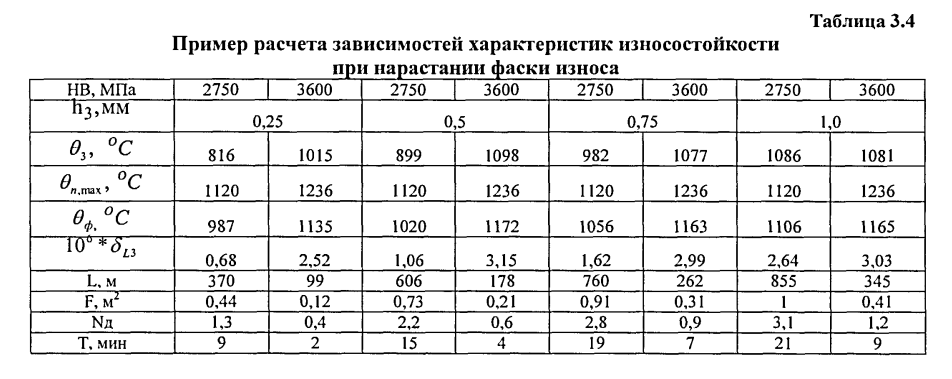
Эти результаты могут быть представлены в табличной форме или в виде графиков.

Кроме указанных данных представлены ранее вычисленные результаты по силам резания, мощности, отклонениям обработанной поверхности и шероховато­сти поверхности. Условия резания для рис. 5-14, приложения 2. те же, что и для табл. 3.3.

Выводы по главе 3

1. Предложена методика оценки процесса восстановления колесных пар на
   основе термомеханического подхода;
2. Получены аналитические зависимости, разработана прикладная про-грамма и создана виртуальная среда для анализа показателей процесса восстанов-ления колесных пар;
3. Выполнен расчет и анализ сил и температур, возникающих в процессе восстановления, для колес с обычной и повышенной твердостью. В качестве ог-раничения для режущего инструмента принята температура формоустойчивости режущего лезвия ~ 870° С;
4. Получены значения температур, сил резания, стойкости инструмента и др. параметров режима резания в зависимости от величины фаски износа.

Список использованной литературы

1. Восстановление профиля поверхности катания колесных пар / И.А. Иванов, М. Ситаж, А.Ф. Богданов; Под ред. д-ра техн. наук И.А. Иванова. — СПб: Петербург¬ский Государственный Университет Путей Сообщения, 2000. — 127 с.
2. Богданов А.Ф., Чурсин В.Г. Эксплуатация и ремонт колесных пар вагонов. — М.: Транспорт, 1985. — 270 с.
3. Иванов И.А. Повышение ресурса колес рельсовых экипажей. Дисс. на соиск. уч. степ, доктора техн. наук. СПб.: ПГУПС, 1993, 257 с.
4. Макаров А. Д. Оптимизация процессов резания. — М.: Машиностроение, 1976, 276 с.
5. Бобров В.Ф., Грановский Г.И., Зорев H.H. и др. Развитие науки о резании ме-таллов. — М.: Машиностроение, 1967, с. 416.
6. Зорев H.H. Расчет проекций сил резания. — М.: Машгиз, 1958, 56 с.
7. Клушин М.И. Резание металлов. — М.: МАШГИЗ, 1958.
8. С.А.Васин, А.С.Верещака, В.С.Кушнер. Резание материалов: Термомеханиче¬ский подход к системе взаимосвязей при резании: Учеб. для техн. вузов.-М.: Изд- во МГТУ им. Н.Э.Баумана, 2001.- 448 с.
9. Силин С.С. Метод подобия при резании материалов. — М.: Машиностроение, 1979, 152 с.
10. Шубин А. А. Оптимизация процесса восстановления профиля поверхности ка-тания вагонных колесных пар. Дисс. на соиск. уч. степ. канд. тех. наук. Л.: ЛИ- ИЖТ. 1986.
11. Резников А.Н., Резников Л.А. Тепловые процессы в технологических систе¬мах: Учебник для вузов по специальности «Технология машиностроения и «Ме-таллорежущие станки и инструменты». М.: Машиностроение, 1990. — 288 е.: с ил.
12. Силин С. С., Верещака А. С., Рыкунов А. И. К вопросу о применении износо-стойких покрытий при точении жаропрочных материалов // Резание и инструмент. — Харьков: Вища школа, 1985. — №33. — с. 81-86.
13. Талантов Н. В. Физические основы процесса резания, изнашивания и разру¬шения инструмента. — М.: Машиностроение, 1992.
14. A.A. Воробьев, П.Г. Сорокин Силы резания при восстановлении профиля обо¬да бандажа чашечными резцами. // Межвузовская научно — техническая конфе¬ренция студентов и молодых ученых: Шаг в будущее (неделя науки — 2004). — СПб. : ПГУПС, 2004. — с. 17.
15. Киселев И.Г. Теплообменные процессы при ремонте колесных пар подвижно¬го состава железных дорог. — Zeszyty naukove Politechniki Slaskiej, №1048, Seria Transport. Z.14. Gliwice: 1989, Str. 131-142.
16. Иванов И.А., Киселев И.Г. и др. Анализ тепловых процессов в технологиче¬ских системах обработки железнодорожных колес. Конструкционно- технологическое обеспечение надежности подвижного состава: Сб. статей. — СПб.: ПГУПС, 1997.-с. 100-111.
17. Бобров В.Ф. Основы теории резания металлов. — М.: Машиностроение, 1975. с. 344.
18. Силин С.С. Применение метода подобия для определения обрабатываемости современных материалов. — Труды Рыбинского авиационно-технологиченского ин-та, №3 -Ярославль, 1975. с. 5-33.
    19 Силин С.С. К вопросу теоретического обоснования автоматизации процессов механической обработки по температуре резания — Труды Ярославльского поли-технического института. — Ярославль, 1976, с. 5-11.
19. Лоладзе Т.Н. Прочность и износостойкость режущего инструмента. -М.: Ма-шиностроение, 1982, 320 с.
20. Иванов И.А. К вопросу оптимизации обработки цельнокатаных колес путем стабилизации температуры резания.- В кн. «Совершенствование технологическо¬го процесса ремонта и формирования колесных пар подвижного состава. — Л.: 1979. с. 97-102.
21. Рекомендации по использованию и назначению параметров режима механиче¬ской обработки при восстановлении профиля поверхности катания вагонных ко¬лес. — М.: ЦВ МПС, 1994, 26 с.
22. Иванов И.А., Урушев C.B., Алешин А.Д. Оптимизация параметров режимов резания цельнокатаных колес./ Zeszyty naukove Politechniki Slaskiej, №1094, Seria Transport. Z.15. Gliwice: 1990, Str. 79-92.
23. И. А. Иванов, А. А. Воробьев, В. С. Кушнер, А. С. Безнин Влияние твердости поверхности катания железнодорожных колес на параметры режима обработки // Новые материалы и технологии в машиностроении. Сборник научных трудов / Под ред. Е.А. Памфилова. — Выпуск 3. — Брянск: БГИТА, 2004. — с. 37 — 41.
24. А. А. Воробьев. О причинах повышенного износа колесных пар подвижного состава и оценка обрабатываемости колес повышенной твердости // Международ¬ная конференция: Транспорт 21 века — Варшава, Польша, 2004. — с. 389 — 397.
25. БапсМк Соготап!;. Токарные инструменты. Каталог С-1000: 2-КШ, 1986.